
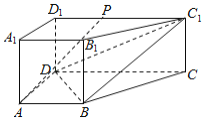
【题目】如图,四棱柱![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是梯形,AB//DC,
是梯形,AB//DC,![]() ,
,![]()

(1).求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的正弦值
的平面角的正弦值
(3).在线段![]() 上是否存在一点
上是否存在一点![]() ,使AP//平面
,使AP//平面![]() .若存在,请确定点
.若存在,请确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)存在点
;(3)存在点![]() 是
是![]() 的中点,使
的中点,使![]() 平面
平面![]() ,证明见解析.
,证明见解析.
【解析】
(1)根据面面垂直的判定定理即可证明平面![]() 平面
平面![]() ;
;
(2)由(1)知![]() ,且
,且![]() 平面
平面![]() ,可知
,可知![]() 为二面角的平面角,在
为二面角的平面角,在![]() 中利用勾股定理得到
中利用勾股定理得到![]() 即可求得
即可求得![]() 的正弦值;
的正弦值;
(3)根据线面平行的判定定理进行证明即可得到结论.
证明:(1)因为![]() 底面
底面![]() ,所以
,所以![]() 底面
底面![]() ,
,
因为![]() 底面
底面![]() ,
,
所以![]() ,
,
因为底面![]() 是梯形,
是梯形,![]() ,
,![]() ,
,
![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]()
所以![]() ,
,![]() ,
,
所以在![]() 中,
中,![]() ,
,
所以![]() ,
,
所以![]() ,
,
又因为![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,
,
(2)由(1)知![]() ,且
,且![]() 平面
平面![]() ,则
,则![]() 为二面角
为二面角![]() 的平面角,
的平面角,
![]() ,
,![]()
由勾股定理可得![]()
![]()
即二面角![]() 的平面角的正弦值为
的平面角的正弦值为![]() .
.
(3)存在点![]() 是
是![]() 的中点,使
的中点,使![]() 平面
平面![]()
证明如下:取线段![]() 的中点为点
的中点为点![]() ,连结
,连结![]() ,
,
所以![]() ,且
,且![]()
因为![]() ,
,![]() ,
,
所以![]() ,且
,且![]()
所以四边形![]() 是平行四边形.
是平行四边形.
所以![]() .
.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.


科目:高中数学 来源: 题型:
【题目】某码头有总重量为![]() 吨的一批货箱,对于每个货箱重量都不超过
吨的一批货箱,对于每个货箱重量都不超过![]() 吨的任何情况,都要一次运走这批货箱,则至少需要准备载重
吨的任何情况,都要一次运走这批货箱,则至少需要准备载重![]() 吨的卡车( )
吨的卡车( )
A.![]() 辆B.
辆B.![]() 辆C.
辆C.![]() 辆D.
辆D.![]() 辆
辆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明非常喜欢葫芦娃七兄弟的人偶玩具,小明的妈妈答应小明买其中的两个,面对红、橙、黄、绿、青、蓝、紫七个造型各异的玩偶小明举棋不定.
(1)请列举出小明购买人偶的所有结果;
(2)事件A为“小明至少从红、橙、黄三个人偶中购买一个”,求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】节能减排以来,兰州市100户居民的月平均用电量![]() 单位:度
单位:度![]() ,以
,以![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

![]() 求直方图中x的值;
求直方图中x的值;![]() 求月平均用电量的众数和中位数;
求月平均用电量的众数和中位数;
![]() 估计用电量落在
估计用电量落在![]() 中的概率是多少?
中的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场销售价与上市时间的关系用图(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图(2)的抛物线段表示.


(1)写出图(1)表示的市场售价与时间的函数关系式![]() 写出图(2)表示的种植成本与时间的函数关系式
写出图(2)表示的种植成本与时间的函数关系式![]()
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?(注:市场售价和种植成本的单位:元/![]() kg,时间单位:天.)
kg,时间单位:天.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某球迷为了解![]() 两支球队的攻击能力,从本赛季常规赛中随机调查了20场与这两支球队有关的比赛.两队所得分数分别如下:
两支球队的攻击能力,从本赛季常规赛中随机调查了20场与这两支球队有关的比赛.两队所得分数分别如下:
![]() 球队:122 110 105 105 109 101 107 129 115 100
球队:122 110 105 105 109 101 107 129 115 100
114 118 118 104 93 120 96 102 105 83
![]() 球队:114 114 110 108 103 117 93 124 75 106
球队:114 114 110 108 103 117 93 124 75 106
91 81 107 112 107 101 106 120 107 79
(1)根据两组数据完成两队所得分数的茎叶图,并通过茎叶图比较两支球队所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
(2)根据球队所得分数,将球队的攻击能力从低到高分为三个等级:
球队所得分数 | 低于100分 | 100分到119分 | 不低于120分 |
攻击能力等级 | 较弱 | 较强 | 很强 |
记事件![]() “
“![]() 球队的攻击能力等级高于
球队的攻击能力等级高于![]() 球队的攻击能力等级”.假设两支球队的攻击能力相互独立. 根据所给数据,以事件发生的频率作为相应事件发生的概率,求
球队的攻击能力等级”.假设两支球队的攻击能力相互独立. 根据所给数据,以事件发生的频率作为相应事件发生的概率,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,点D在棱
,点D在棱![]() 上,且
上,且![]() ,建立如图所示的空间直角坐标系.
,建立如图所示的空间直角坐标系.

(1)当![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 的夹角的余弦值;
的夹角的余弦值;
(2)若二面角![]() 的平面角为
的平面角为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在各棱长均为2的三棱柱![]() 中,侧面
中,侧面![]() 底面ABC,
底面ABC,![]() .
.
(1)求侧棱![]() 与平面
与平面![]() 所成角的正弦值的大小;
所成角的正弦值的大小;
(2)已知点D满足![]() ,在直线
,在直线![]() 上是否存在点P,使DP∥平面
上是否存在点P,使DP∥平面![]() ?若存在,请确定点P的位置,若不存在,请说明理由.
?若存在,请确定点P的位置,若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求函数![]() 的单调增区间;最大值,以及取得最大值时x的取值集合;
的单调增区间;最大值,以及取得最大值时x的取值集合;
(2)已知![]() 中,角A、B、C的对边分别为a,b,c,若
中,角A、B、C的对边分别为a,b,c,若![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com