
分析 (1)根据函数单调性的定义以及“保值函数”的定义判断即可;
(2)由f(x)的定义域和值域都是[m,n],问题等价于方程a2x2-(2a2+a)x+1=0有两个不等的实数根,根据根的判别式判断即可;
(3)由不等式|a2f(x)|≤2x对x≥1恒成立,令h(x)=2x+$\frac{1}{x}$,易证h(x)在[1,+∞)递增,同理g(x)=$\frac{1}{x}$-2x[1,+∞)递减,求出函数h(x)min,与函数g(x)max,建立不等关系,解之即可求出a的范围.
解答 解:(1)g(x)=x2-2x=(x-1)2-1,
x∈[0,1]时,g(x)∈[-1,0],
根据函数g(x)不是定义域[0,1]上的“保值函数”.
(2))由f(x)的定义域和值域都是[m,n]得f(m)=m,f(n)=n,
因此m,n是方程2+$\frac{1}{a}$-$\frac{1}{{a}^{2}x}$=x的两个不相等的实数根,
等价于方程a2x2-(2a2+a)x+1=0有两个不等的实数根,
即△=(2a2+a)2-4a2>0
解得a>$\frac{1}{2}$或a<-$\frac{3}{2}$;
(3)a2f(x)=2a2+a-$\frac{1}{x}$,则不等式|a2f(x)|≤2x对x≥1恒成立,
即-2x≤2a2+a-$\frac{1}{x}$≤2x即不等式对x≥1恒成立,
令h(x)=2x+$\frac{1}{x}$,易证h(x)在[1,+∞)递增,
同理g(x)=$\frac{1}{x}$-2x[1,+∞)递减,
∴h(x)min=h(1)=3,g(x)max=g(1)=-1,
∴$\left\{\begin{array}{l}{{2a}^{2}+a≤3}\\{{2a}^{2}+a≥-1}\end{array}\right.$,
∴-$\frac{3}{2}$≤a≤1且a≠0.
点评 本题主要考查了函数单调性的判断与证明,以及函数恒成立问题和不等式的综合,同时考查了转化与划归的思想,属于综合题.


科目:高中数学 来源: 题型:填空题
 如图,已知正方体ABC-A1B1C1D1中,AB=a,P为线段BC1上一点,Q为平面ABCD内一点,则D1P+PQ的最小值为(1+$\frac{\sqrt{2}}{2}$)a.
如图,已知正方体ABC-A1B1C1D1中,AB=a,P为线段BC1上一点,Q为平面ABCD内一点,则D1P+PQ的最小值为(1+$\frac{\sqrt{2}}{2}$)a.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {1,2} | C. | {0} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
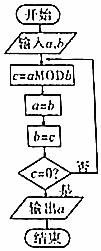 “欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前,如图的程序框图的算法思路就是来源于“欧几里得算法”.执行改程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为675,125,则输出的a=( )
“欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前,如图的程序框图的算法思路就是来源于“欧几里得算法”.执行改程序框图(图中“aMODb”表示a除以b的余数),若输入的a,b分别为675,125,则输出的a=( )| A. | 0 | B. | 25 | C. | 50 | D. | 75 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 12 | D. | 6+$\sqrt{29}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com