Question

16．已知点（2，5）和（8，3）是函数y=-k|x-a|+b与y=k|x-c|+d的图象仅有的两个交点，那么a+b+c+d的值为18．

Answer 1

分析 将两个交点代入函数y=-k|x-a|+b方程，得到方程组，将两个方程相减；据绝对值的意义及k的范围得到k，a满足的等式；同样的过程得到k，c满足的等式，两式联立求出a+c的值，再求出b+d，即可得到结论．

解答 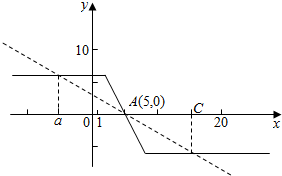解：∵函数y=-k|x-a|+b与y=k|x-c|+d的图象交于两点（2，5），（8，3），
∴5=-k|2-a|+b ①
3=-k|8-a|+b ②
5=k|2-c|+d ③
3=k|8-c|+d ④
①-②得2=-k|2-a|+k|8-a|⑤
③-④得2=k|2-c|-k|8-c|⑥
⑤=⑥得|8-a|+|8-c|=|2-c|+|2-a|
即|8-a|-|2-a|+|8-c|-|2-c|=0
设f（x）=|8-x|-|2-x|，则f（a）+f（c）=0，
画出函数f（x）的图象，如图，其关于点A（5，0）成中心对称，
故点a与点c关于点A（5，0）成中心对称，
∴$\frac{1}{2}$（a+c）=5，
∴a+c=10，
又∵函数y=-k|x-a|+b的对称轴为x=a，函数y=k|x-c|+d的对称轴为x=c，
∴2＜a＜8，2＜c＜8
②+③：8=-k（8-a）+b+k（c-2）+d，
∴b+d=8，
∴a+b+c+d=18
故答案为：18．

点评 本题考查函数的图象，考查绝对值的意义，考查学生分析解决问题的能力，属于中档题．