
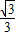 ,
, )
) ,0)∪(0,
,0)∪(0, )
) ,
, ]
] )∪(
)∪( ,+∞)
,+∞)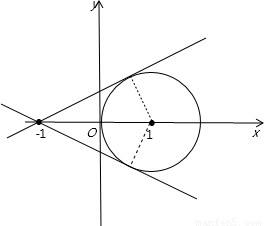 解:由题意可知曲线C1:x2+y2-2x=0表示一个圆,化为标准方程得:
解:由题意可知曲线C1:x2+y2-2x=0表示一个圆,化为标准方程得: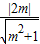 =r=1,
=r=1, ,解得m=±
,解得m=±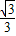 ,
,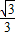 ,0)∪(0,
,0)∪(0,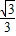 ).
).

科目:高中数学 来源: 题型:
A、(-
| ||||||||
B、(-
| ||||||||
C、[-
| ||||||||
D、(-∞,-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省济宁市泗水一中高三(上)期末数学模拟试卷(理科)(解析版) 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省教育学院附中高三(上)11月月考数学试卷(理科)(解析版) 题型:选择题
 ,
, )
) ,0)∪(0,
,0)∪(0, )
) ,
,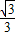 ]
] )∪(
)∪( ,+∞)
,+∞)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com