【题目】已知函数
.
（Ⅰ）求
的极值；
（Ⅱ）若函数
的图像与函数
的图像在区间
上有公共点，求实数
的取值范围.
【答案】（1）极小值为
，无极大值.（2）
【解析】试题分析：(Ⅰ)函数求导,令
,求出根,分析其两侧导数的符号,确定函数的极值;(Ⅱ)若函数
的图象与函数
的图象在区间
上有公共点,转化为求函数
在区间
上的值域,根据(Ⅰ)分类讨论函数在区间
是的单调性,确定函数
的最值.
试题解析：
（1）函数
的定义域为
， 
，令
，得
，
当
时， 
， 
是减函数；
当
时， 
， 
是增函数.
所以当
时， 
取得极小值，即极小值为
，无极大值.
（2）①当
，即
时，由（1）知， 
在
上是减函数，在
上增函数，当
时， 
取得最小值，即
最小值
，又当
时， 
，当
时， 
，当
时， 
，所以
的图像与函数
的图像在区间
上有公共点，等价于
，解得
，又
，所以
.
②当
，即
时， 
在
上是减函数， 
在
上的最小值为
，所以，原问题等价于
，得
，又
，所以不存在这样的实数
.综上知实数
的取值范围是
.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】某单位职工义务献血，在体检合格的人中， 
型血的共有28人， 
型血的共有7人， 
型血的共有9人， 
型血的有3人．
（1）从中任选1人去献血，有多少种不同的选法？
（2）从四种血型的人中各选1人去献血，有多少种不同的选法？
查看答案和解析>>
科目：高中数学 来源： 题型：
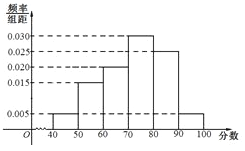
【题目】上周某校高三年级学生参加了数学测试，年部组织任课教师对这次考试进行成绩分析.现从中抽取80名学生的数学成绩（均为整数）的频率分布直方图如图所示.
（Ⅰ）估计这次月考数学成绩的平均分和众数；
（Ⅱ）假设抽出学生的数学成绩在
段各不相同，且都超过94分.若将频率视为概率，现用简单随机抽样的方法，从95，96，97，98，99，100这6个数字中任意抽取2个数，有放回地抽取3次，记这3次抽取中恰好有两名学生的数学成绩的次数为
，求
的分布列和期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】【2015高考湖北】如图，圆C与x轴相切于点T(1，0)，与y轴正半轴交于两点A，B(B在A的上方)，且|AB|＝2.
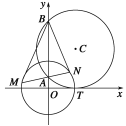
(1)圆C的标准方程为________．
(2)过点A任作一条直线与圆O：x2＋y2＝1相交于M，N两点，下列三个结论：
①
＝
；②
－＝2；
③＋＝2
.
其中正确结论的序号是________(写出所有正确结论的序号)．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
（x∈R），给出下面四个命题：
①函数f（x）的图象一定关于某条直线对称；
②函数f（x）在R上是周期函数；
③函数f（x）的最大值为 
；
④对任意两个不相等的实数 
，都有 
成立．
其中所有真命题的序号是 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
， 
（
）.
（Ⅰ）求函数
的单调增区间；
（Ⅱ）当
时，记
，是否存在整数
，使得关于
的不等式
有解？若存在，请求出
的最小值；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设数列
的前n项和为
，已知
（p、q为常数， 
），又
， 
， 
.
（1）求p、q的值；
（2）求数列
的通项公式；
（3）是否存在正整数m、n，使
成立？若存在，求出所有符合条件的有序实数对
；若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，某公园有三条观光大道
围成直角三角形，其中直角边
，斜边
．现有甲、乙、丙三位小朋友分别在
大道上嬉戏，所在位置分别记为点
．
（1）若甲乙都以每分钟
的速度从点
出发在各自的大道上奔走，到大道的另一端
时即停，乙比甲迟2分钟出发，当乙出发1分钟后，求此时甲乙两人之间的距离；
（2）设
，乙丙之间的距离是甲乙之间距离的2倍，且
，请将甲
乙之间的距离
表示为θ的函数，并求甲乙之间的最小距离．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
