
【题目】已知两个平面![]() ,
,![]() 相互垂直,
相互垂直,![]() 是它们的交线,则下面结论正确的是( )
是它们的交线,则下面结论正确的是( )
A.垂直于平面![]() 的平面一定平行于平面
的平面一定平行于平面![]()
B.垂直于直线![]() 的平面一定平行于平面
的平面一定平行于平面![]()
C.垂直于平面![]() 的平面一定平行于直线
的平面一定平行于直线![]()
D.垂直于直线![]() 的平面一定与平面
的平面一定与平面![]() ,
,![]() 都垂直
都垂直
 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
【题目】三棱柱![]() 的主视图和俯视图如图所示(图中一格为单位正方形),D、D1分别为棱AC和A1C1的中点.
的主视图和俯视图如图所示(图中一格为单位正方形),D、D1分别为棱AC和A1C1的中点.
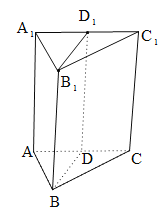
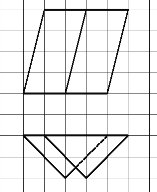
(1)求侧(左)视图的面积,并证明平面A1ACC1⊥平面B1BDD1
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面坐标系中xOy中,已知直线l的参数方程为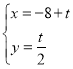 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为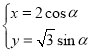 (
(![]() 为参数).以O为极点,x轴的非负半轴为极轴,建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴,建立极坐标系.
(1)求曲线C的普通方程和直线l的极坐标方程;
(2)设P为曲线C上的动点,求点P到直线l的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 上任一点
上任一点![]() 到
到![]() ,
,![]() 的距离之和为4.
的距离之和为4.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,设直线
,设直线![]() 不经过
不经过![]() 点,
点,![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,若直线
两点,若直线![]() 的斜率与直线
的斜率与直线![]() 的斜率之和为
的斜率之和为![]() ,判断直线
,判断直线![]() 是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“总把新桃换旧符”(王安石)、“灯前小草写桃符”(陆游),春节是中华民族的传统节日.在宋代人们用写“桃符”的方式来祈福避祸,而现代人们通过贴“福”字、春联等方式来表达对新年的美好祝愿.某商家在春节前开展商品促销活动,顾客凡购物金额满50元,则可以任意免费领取一张“福”字或一副春联。茎叶图的统计数据是在不同时段内领取“福”字和春联的人数,则它们的中位数依次为( )
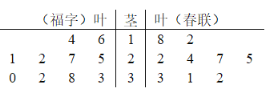
A.25,27B.26,25C.26,27D.27,25
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),其中
为参数),其中![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,与
,与![]() 交于
交于![]() 两点,且
两点,且![]() ,求
,求![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解居民的用电情况,某地供电局抽查了该市若干户居民月均用电量(单位:![]() ),并将样本数据分组为
),并将样本数据分组为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其频率分布直方图如图所示.
,其频率分布直方图如图所示.
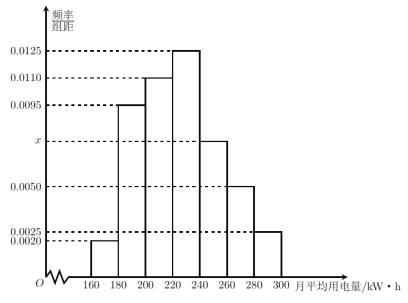
(1)若样本中月均用电量在![]() 的居民有
的居民有![]() 户,求样本容量;
户,求样本容量;
(2)求月均用电量的中位数;
(3)在月均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组居民中,用分层随机抽样法抽取
的四组居民中,用分层随机抽样法抽取![]() 户居民,则月均用电量在
户居民,则月均用电量在![]() 的居民应抽取多少户?
的居民应抽取多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com