
分析 (1)根据f(x)为奇函数便知,f(x)的定义域关于原点对称,从而求出定义域为(-3,a),从而得出a=3;
(2)得出f(x)=$lo{g}_{\frac{1}{3}}\frac{3-x}{x+3}$=$lo{g}_{\frac{1}{3}}(-1+\frac{6}{x+3})$,根据-3<x<3便可得出$\frac{1}{x+3}$的范围,进一步得出$-1+\frac{6}{x+3}>0$,这样根据对数函数的值域便可得出函数f(x)的值域.
解答 解:(1)f(x)为奇函数,∴定义域关于原点对称;
∴解$\left\{\begin{array}{l}{a-x>0}\\{x+3>0}\end{array}\right.$得,-3<x<a;
∴a=3;
(2)$f(x)=lo{g}_{\frac{1}{3}}(3-x)-lo{g}_{\frac{1}{3}}(x+3)$=$lo{g}_{\frac{1}{3}}\frac{3-x}{x+3}=lo{g}_{\frac{1}{3}}(-1+\frac{6}{x+3})$;
∵-3<x<3;
∴0<x+3<6,$\frac{1}{x+3}>\frac{1}{6}$;
∴$-1+\frac{6}{x+3}>0$;
∴f(x)的值域为R.
点评 考查奇函数的定义,奇函数的定义域的特点,对数的运算,分离常数法的运用,以及对数函数的值域.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:选择题
| A. | y=log2(x+1) | B. | y=log2(x-1) | C. | y=log2x+1 | D. | y=log2x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
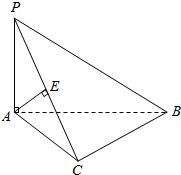 如图,已知PA⊥平面ABC,∠ACB=90°,AP=AC,E为PC的中点.求证:
如图,已知PA⊥平面ABC,∠ACB=90°,AP=AC,E为PC的中点.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com