
【题目】已知M是椭圆C:![]() +
+![]() =1(a>b>0)上一点,F1F2分别为椭圆C的左右焦点,且|F1F2|=2,∠F1MF2=
=1(a>b>0)上一点,F1F2分别为椭圆C的左右焦点,且|F1F2|=2,∠F1MF2=![]() ,△F1MF2的面积为
,△F1MF2的面积为![]() .
.
(1)求椭圆C的方程;
(2)直线l过椭圆C右焦点F2,交该椭圆于AB两点,AB中点为Q,射线OQ交椭圆于P,记△AOQ的面积为S1,△BPQ的面积为S2,若![]() ,求直线l的方程.
,求直线l的方程.
【答案】(1)![]() +
+![]() =1;(2)
=1;(2)![]() .
.
【解析】
(1)根据 |F1F2|=2,得到c=1,设![]() 根据∠F1MF2=
根据∠F1MF2=![]() ,△F1MF2的面积为
,△F1MF2的面积为![]() ,
,![]() ,得到
,得到![]() ,然后在
,然后在![]() 中,由余弦定理结合椭圆的定义解得
中,由余弦定理结合椭圆的定义解得 ![]() ,求得
,求得![]() 即可.
即可.
(2)根据![]() ,由
,由![]() ,得到
,得到![]() ,从而
,从而![]() ,当AB斜率不存在时,
,当AB斜率不存在时,![]() ,不合题意,当AB斜率存在时,设直线方程为
,不合题意,当AB斜率存在时,设直线方程为![]() ,设点
,设点![]() ,则
,则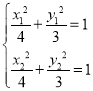 ,两式作差得到
,两式作差得到![]() ,故设直线OP的方程为:
,故设直线OP的方程为:![]() ,分别联立椭圆方程和直线AB的方程,求得点P,Q的坐标,由
,分别联立椭圆方程和直线AB的方程,求得点P,Q的坐标,由![]() 求解.
求解.
(1)因为 |F1F2|=2,
所以c=1,设![]()
![]() ,
,
因为∠F1MF2=![]() ,△F1MF2的面积为
,△F1MF2的面积为![]() ,
,
所以![]() ,
,
所以![]() ,
,
在![]() 中,由余弦定理得:
中,由余弦定理得:![]() ,
,
即![]() ,
,
解得![]() ,
,
所以![]() ,
,
所以椭圆C的方程是![]() +
+![]() =1.
=1.
(2)因为![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
当AB斜率不存在时,![]() ,不合题意,
,不合题意,
当AB斜率存在时,设直线方程为![]() ,
,
设点![]() ,
,
则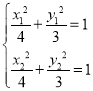 ,
,
两式作差得:![]() ,即
,即![]() ,
,
故直线OP的方程为:![]() ,
,
联立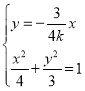 ,解得
,解得![]() ,
,
联立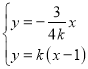 ,解得
,解得![]() ,
,
因为![]() ,
,
所以![]() ,
,
即![]() ,
,
解得:![]() ,
,
所以直线AB的方程为![]() .
.


 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线C:
是抛物线C:![]() 上的一点,过P作互相垂直的直线PA,PB.与抛物线C的另一交点分别是A,B.
上的一点,过P作互相垂直的直线PA,PB.与抛物线C的另一交点分别是A,B.
(1)若直线AB的斜率为![]() ,求AB方程;
,求AB方程;
(2)设![]() ,当
,当![]() 时,求△PAB的面积.
时,求△PAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某景区平面图如图1所示,![]() 为边界上的点.已知边界
为边界上的点.已知边界![]() 是一段抛物线,其余边界均为线段,且
是一段抛物线,其余边界均为线段,且![]() ,抛物线顶点
,抛物线顶点![]() 到
到![]() 的距离
的距离![]() .以
.以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系.
轴,建立平面直角坐标系.
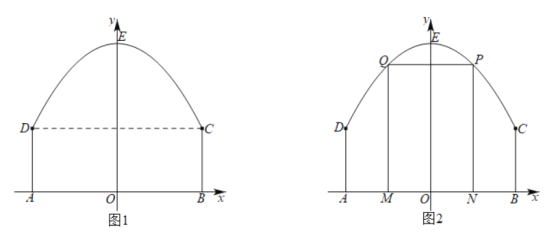
(1)求边界![]() 所在抛物线的解析式;
所在抛物线的解析式;
(2)如图2,该景区管理处欲在区域![]() 内围成一个矩形
内围成一个矩形![]() 场地,使得点
场地,使得点![]() 在边界
在边界![]() 上,点
上,点![]() 在边界
在边界![]() 上,试确定点
上,试确定点![]() 的位置,使得矩形
的位置,使得矩形![]() 的周长最大,并求出最大周长.
的周长最大,并求出最大周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上,![]() ,
,![]() ,且
,且![]() 的离心率为
的离心率为![]() ,抛物线
,抛物线![]() ,点
,点![]() 在
在![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作
作![]() 的切线
的切线![]() ,若
,若![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京2022年冬奥会和冬残奥会色彩系统的主色包括霞光红迎春黄天霁蓝长城灰瑞雪白;间色包括天青梅红竹绿冰蓝吉柿;辅助色包括墨金银.若各赛事纪念品的色彩设计要求:主色至少一种至多两种,间色两种辅助色一种,则某个纪念品的色彩搭配中包含有瑞雪白冰蓝银色这三种颜色的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的普通方程为
的普通方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),其中
为参数),其中![]() .以坐标
.以坐标![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴,建立极坐标系.
轴非负半轴为极轴,建立极坐标系.
(1)求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设点![]() ,
,![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与
与![]() 的交点分别为
的交点分别为![]() ,
,![]() .当
.当![]() 为等腰直角三角形时,求直线
为等腰直角三角形时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记无穷数列![]() 的前n项
的前n项![]() ,
,![]() ,…,
,…,![]() 的最大项为
的最大项为![]() ,第n项之后的各项
,第n项之后的各项![]() ,
,![]() ,…的最小项为
,…的最小项为![]() ,
,![]() .
.
(1)若数列![]() 的通项公式为
的通项公式为![]() ,写出
,写出![]() ,
,![]() ,
,![]() ;
;
(2)若数列![]() 的通项公式为
的通项公式为![]() ,判断
,判断![]() 是否为等差数列,若是,求出公差;若不是,请说明理由;
是否为等差数列,若是,求出公差;若不是,请说明理由;
(3)若数列![]() 为公差大于零的等差数列,求证:
为公差大于零的等差数列,求证:![]() 是等差数列.
是等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com