
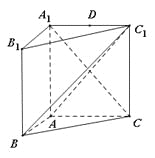
【题目】如图,在直三棱柱![]() 中,
中,![]() ,且
,且![]() .
.
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)设![]() 是
是![]() 的中点,判断并证明在线段
的中点,判断并证明在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() ‖平面
‖平面![]() ;若存在,求三棱锥
;若存在,求三棱锥![]() 的体积.
的体积.
【答案】(1)证明详见解析;(2)![]() .
.
【解析】试题分析:本题以直三棱柱为几何背景,考查线线垂直、线面垂直、面面垂直、面面平行、线面平行、三棱锥的体积等基础知识,考查学生的空间想象能力、逻辑推理能力、计算能力.第一问,要证平面![]() ⊥平面
⊥平面![]() ,需要证
,需要证![]() 平面
平面![]() ;第二问,作出辅助线,通过3边都平行,利用面面平行的判定得到面EFD//平面
;第二问,作出辅助线,通过3边都平行,利用面面平行的判定得到面EFD//平面![]() ,再利用面面平行的性质得DE//平面
,再利用面面平行的性质得DE//平面![]() ,由于
,由于![]() 平面
平面![]() ,所以
,所以![]() 是三棱锥
是三棱锥![]() 的高,所以将
的高,所以将![]() 转化为
转化为![]() ,再求解.
,再求解.
试题解析:(1)∵直三棱柱侧面为矩形,且![]() ,
,
∴四边形![]() 为正方形,
为正方形,
∴![]() ,
,
∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]()
∵![]() 平面
平面![]()
∴平面![]() ⊥平面
⊥平面![]() ; .5分
; .5分
(2)分别取![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]()
![]() 平面
平面![]() ∥平面
∥平面![]() ,
,![]()
![]() ‖平面
‖平面![]() , .8分
, .8分
![]()
![]() 平面
平面![]() , .10分
, .10分
![]()
![]() .12分
.12分


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:
【题目】下列说法中,正确的个数为( )
(1) ![]()
(2)已知向量 ![]() =(6,2)与
=(6,2)与 ![]() =(﹣3,k)的夹角是钝角,则k的取值范围是k<0
=(﹣3,k)的夹角是钝角,则k的取值范围是k<0
(3)若向量 ![]() 能作为平面内所有向量的一组基底
能作为平面内所有向量的一组基底
(4)若 ![]() ,则
,则 ![]() 在
在 ![]() 上的投影为
上的投影为 ![]() .
.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=f(x)的图象如图所示.观察图象可知函数y=f(x)的定义域、值域分别是( )
A.[﹣5,0]∪[2,6),[0,5]
B.[﹣5,6),[0,+∞)
C.[﹣5,0]∪[2,6),[0,+∞)
D.[﹣5,+∞),[2,5]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x|,g(x)=lg(ax2﹣4x+1),若对任意x1∈R,都存在在x2∈R,使f(x1)=g(x2),则实数a的取值范围是( )
A.(﹣∞,4]
B.(0,4]
C.(﹣4,0]
D.[0,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() 、
、![]() 、
、![]() ,如果存在实数
,如果存在实数![]() 使得
使得![]() ,那么称
,那么称![]() 为
为![]() 、
、![]() 的生成函数.
的生成函数.
(1) 下面给出两组函数, ![]() 是否分别为
是否分别为![]() 、
、![]() 的生成函数?并说明理由;
的生成函数?并说明理由;
第一组: ![]() ,
, ![]() ,
, ![]()
第二组: ![]() ,
, ![]() ,
, ![]() ;
;
(2) 设![]() ,
, ![]() ,
, ![]() ,生成函数
,生成函数![]() .若不等式
.若不等式![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3) 设![]() ,
, ![]() ,取
,取![]() ,生成函数
,生成函数![]() 图像的最低点坐标为
图像的最低点坐标为![]() .若对于任意正实数
.若对于任意正实数![]() ,且
,且![]() ,试问是否存在最大的常数
,试问是否存在最大的常数![]() ,使
,使![]() 恒成立?如果存在,求出这个
恒成立?如果存在,求出这个![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1的离心率为
=1的离心率为 ![]() ,焦距为2,右焦点为F,过点F的直线交椭圆于A、B两点.
,焦距为2,右焦点为F,过点F的直线交椭圆于A、B两点.
(1)求椭圆C的方程;
(2)在x轴上是否存在定点M,使得 ![]() 为定值?若存在,求出定值和定点坐标;若不存在,请说明理由.
为定值?若存在,求出定值和定点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=﹣x2+(3﹣2m)x+2+m(0<m≤1).
(1)若x∈[0,m],证明:f(x)≤ ![]() ;
;
(2)求|f(x)|在[﹣1,1]上的最大值g(m).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com