
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 在
在![]() 上且
上且![]() .
.
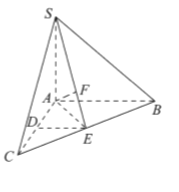
(I)求证:![]() ;
;
(II)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(III)在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】I.见解析;Ⅱ.![]() ;Ⅲ.满足条件的点G存在,且
;Ⅲ.满足条件的点G存在,且![]()
【解析】
I:建立空间坐标系,求出相应的直线的方向向量和平面的法向量,证明向量的平行即可;Ⅱ:求出平面SBD的法向量,直线SA的方向向量,由公式可得到线面角;Ⅲ.假设满足条件的点G存在,并设DG=1.则G(1,t,0),求出平面AFG的法向量,和面AFE的法向量,由二面角的平面角的公式得到关于t的方程,进而求解.
I.以A为坐标原点,分别以AC,AB.AS为x,y,z轴建立空间直角坐标系C-xyz.则A(0,0,0),B(0,2,0),C(2,0,0),S(0,0,2),D(1,0,0),E(1,1,0)
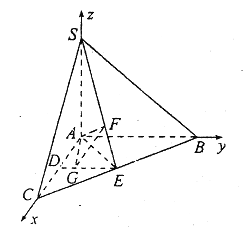
由SF=2FE得F(![]() ,
,![]() ,
,![]() )
)
![]()
![]() 平面
平面
![]()
![]()
![]() 平面SBC
平面SBC
Ⅱ.设![]() (x1,y1,z1)是平面SBD的一个法向量,
(x1,y1,z1)是平面SBD的一个法向量,
由于![]() ,则有
,则有

令![]() ,则
,则![]() ,即
,即![]() 。
。
设直线SA与平面SBD所成的角为![]() ,而
,而![]() ,
,
所以
Ⅲ.假设满足条件的点G存在,并设DG=![]() .则G(1,t,0).
.则G(1,t,0).
所以![]()
设平面AFG的法向量为![]() ,
,
则
取![]() ,得
,得![]()
即![]() .
.
设平面AFE的法向量为![]()
则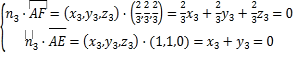
取![]() ,得
,得![]() ,即
,即![]()
由得二面角G-AF-E的大小为![]() 得
得
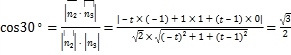 ,化简得
,化简得![]() ,
,
又![]() ,求得
,求得![]() ,于是满足条件的点G存在,且
,于是满足条件的点G存在,且![]()


科目:高中数学 来源: 题型:
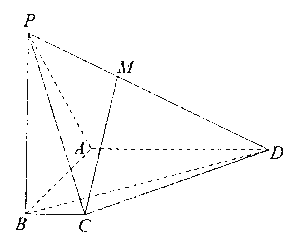
【题目】如图,在四棱锥![]() 中:
中:![]() 底面ABCD,底面ABCD为梯形,
底面ABCD,底面ABCD为梯形,![]() ,
,![]() ,且
,且![]() ,BC=1,M为棱PD上的点。
,BC=1,M为棱PD上的点。
(Ⅰ)若![]() ,求证:CM∥平面PAB;
,求证:CM∥平面PAB;
(Ⅱ)求证:平面![]() 平面PAB;
平面PAB;
(Ⅲ)求直线BD与平面PAD所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知8件不同的产品中有3件次品,现对它们一一进行测试,直至找到所有次品.
(1)若恰在第2次测试时,找到第一件次品,第6次测试时,才找到最后一件次品,则共有多少种不同的测试方法?
(2)若至多测试5次就能找到所有次品,则共有多少种不同的测试方法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右顶点是双曲线
的左右顶点是双曲线![]() 的顶点,且椭圆
的顶点,且椭圆![]() 的上顶点到双曲线
的上顶点到双曲线![]() 的渐近线的距离为
的渐近线的距离为![]() 。
。
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 相交于
相交于![]() 两点,与
两点,与![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,(
,(![]() 为常数)
为常数)
(1)若![]()
①求函数![]() 在区间
在区间![]() 上的最大值及最小值。
上的最大值及最小值。
②若过点![]() 可作函数
可作函数![]() 的三条不同的切线,求实数
的三条不同的切线,求实数![]() 的取值范围。
的取值范围。
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,![]() E是PD的中点.
E是PD的中点.
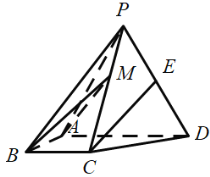
(1)证明:直线![]() 平面PAB;
平面PAB;
(2)点M在棱PC 上,且直线BM与底面ABCD所成角为![]() ,求二面角M-AB-D的余弦值.
,求二面角M-AB-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)的最小值为﹣4,且关于x的不等式f(x)≤0的解集为{x|﹣1≤x≤3,x∈R}.
(1)求函数f(x)的解析式;
(2)求函数g(x)![]() 的零点个数.
的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机的普及,使用手机上网成为了人们日常生活的一部分,很多消费者对手机流量的需求越来越大.长沙某通信公司为了更好地满足消费者对流量的需求,准备推出一款流量包.该通信公司选了5个城市(总人数、经济发展情况、消费能力等方面比较接近)采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价![]() :(单位:元/月)和购买人数
:(单位:元/月)和购买人数![]() (单位:万人)的关系如表:
(单位:万人)的关系如表:
![]()
(1)根据表中的数据,运用相关系数进行分析说明,是否可以用线性回归模型拟合![]() 与
与![]() 的关系?并指出是正相关还是负相关;
的关系?并指出是正相关还是负相关;
(2)①求出![]() 关于
关于![]() 的回归方程;
的回归方程;
②若该通信公司在一个类似于试点的城市中将这款流量包的价格定位25元/ 月,请用所求回归方程预测长沙市一个月内购买该流量包的人数能否超过20 万人.
参考数据:![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数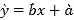 ,回归直线方程
,回归直线方程![]() ,
,
其中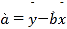 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com