
【题目】已知定圆![]() ,动圆
,动圆![]() 过点
过点![]() 且与圆
且与圆![]() 相切,记动圆圆心
相切,记动圆圆心![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程
的方程
(2)若轨迹![]() 上存在两个不同点
上存在两个不同点![]() ,
,![]() 关于直线
关于直线![]() 对称,求
对称,求![]() 面积的最大值(
面积的最大值(![]() 为坐标原点).
为坐标原点).
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据![]() 在圆
在圆![]() 内,所以圆
内,所以圆![]() 内切于圆
内切于圆![]() ,则有
,则有![]() ,即
,即![]() ,根据椭圆的定义,可知点
,根据椭圆的定义,可知点![]() 的轨迹
的轨迹![]() 是椭圆再求解.
是椭圆再求解.
(2)根据![]() ,
,![]() 关于直线
关于直线![]() 对称,直线
对称,直线![]() 的方程为
的方程为![]() ,与椭圆方程联立
,与椭圆方程联立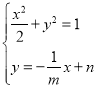 消去
消去![]() ,得
,得![]() ,根据直线
,根据直线![]() 与椭圆
与椭圆![]() 有两个不同的交点,
有两个不同的交点,![]() ,
,![]() 的中点
的中点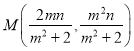 在直线
在直线![]() 上,得到
上,得到![]() 的取值范围,再利用
的取值范围,再利用 ![]() 求解.
求解.
(1)因为![]() 在圆
在圆![]() 内,所以圆
内,所以圆![]() 内切于圆
内切于圆![]() ,
,
所以![]()
即![]() ,
,
所以点![]() 的轨迹
的轨迹![]() 是以
是以![]() 和
和![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆,
的椭圆,
因为![]() ,
,![]() ,所以
,所以![]() ,
,
所以点![]() 的轨迹方程为:
的轨迹方程为:![]() ;
;
(2)由题意知![]() ,可设直线
,可设直线![]() 的方程为
的方程为![]() ,
,
由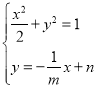 消去
消去![]() ,得
,得![]() ,
,
因为直线![]() 与椭圆
与椭圆![]() 有两个不同的交点,所以
有两个不同的交点,所以![]() ,①
,①
所以![]() 中点
中点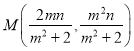 ,代入直线方程
,代入直线方程![]() ,解得
,解得![]() ,②
,②
由①②解得![]() ,或
,或![]() ,
,
令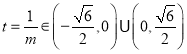 ,则
,则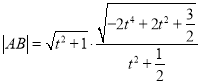 ,
,
且![]() 到直线
到直线![]() 的距离为
的距离为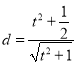 ,
,
设![]() 的面积为
的面积为![]() ,
,
所以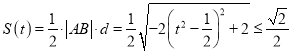 ,当且仅当
,当且仅当![]() 时,等号成立,
时,等号成立,
所以![]() 面积的最大值为
面积的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】定义[x]表示不超过x的最大整数,![]() ,例如:
,例如:![]() .执行如图所示的程序框图若输入的
.执行如图所示的程序框图若输入的![]() ,则输出结果为( )
,则输出结果为( )
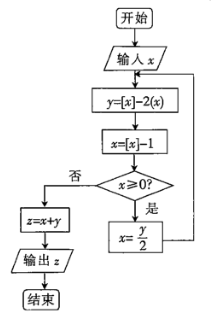
A.-4.6B.-2.8C.-1.4D.-2.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年初,某高级中学教务处为了解该高级中学学生的作文水平,从该高级中学学生某次考试成绩中按文科、理科用分层抽样方法抽取![]() 人的成绩作为样本,得到成绩频率分布直方图如图所示,
人的成绩作为样本,得到成绩频率分布直方图如图所示,![]() ,参考的文科生与理科生人数之比为
,参考的文科生与理科生人数之比为![]() ,成绩(单位:分)分布在
,成绩(单位:分)分布在![]() 的范围内且将成绩(单位:分)分为
的范围内且将成绩(单位:分)分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六个部分,规定成绩分数在
六个部分,规定成绩分数在![]() 分以及
分以及![]() 分以上的作文被评为“优秀作文”,成绩分数在50分以下的作文被评为“非优秀作文”.
分以上的作文被评为“优秀作文”,成绩分数在50分以下的作文被评为“非优秀作文”.

(1)求实数![]() 的值;
的值;
(2)(i)完成下面![]() 列联表;
列联表;
文科生/人 | 理科生/人 | 合计 | |
优秀作文 | 6 | ______ | ______ |
非优秀作文 | ______ | ______ | ______ |
合计 | ______ | ______ | 400 |
(ii)以样本数据研究学生的作文水平,能否在犯错误的概率不超过![]() 的情况下认为获得“优秀作文”与学生的“文理科“有关?
的情况下认为获得“优秀作文”与学生的“文理科“有关?
注: ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次数学知识比赛中共有6个不同的题目,每位同学从中随机抽取3个题目进行作答,已知这6个题目中,甲只能正确作答其中的4个,而乙正确作答每个题目的概率均为![]() ,且甲、乙两位同学对每个题目的作答都是相互独立、互不影响的.
,且甲、乙两位同学对每个题目的作答都是相互独立、互不影响的.
(1)求甲、乙两位同学总共正确作答3个题目的概率;
(2)若甲、乙两位同学答对题目个数分别是![]() ,
,![]() ,由于甲所在班级少一名学生参赛,故甲答对一题得15分,乙答对一题得10分,求甲乙两人得分之和
,由于甲所在班级少一名学生参赛,故甲答对一题得15分,乙答对一题得10分,求甲乙两人得分之和![]() 的期望.
的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),圆
为参数),圆![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)过直线![]() 上的一点
上的一点![]() 作一条倾斜角为
作一条倾斜角为![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着生活节奏的加快以及停车日益困难,网约车越来越受到大众的欢迎.某网约车公司为了了解客户对公司的满意度,通过网络问卷的方式,随机调查了2000个客户,并通过随机抽样得到100个样本数据,统计后,得到如下频率分布表:
分组 |
|
|
|
|
|
|
|
频数 | 6 | 12 | 19 | 25 | 20 | 13 | 5 |
(1)根据频率分布表,可以认为满意度![]() ,其中
,其中![]() 近似看作是这100个样本数据的平均值,利用正态分布,求
近似看作是这100个样本数据的平均值,利用正态分布,求![]() ;
;
(2)该公司为参加网络问卷调查的客户提供了抽奖活动,活动规则:①若满意度不低于![]() ,可抽奖2次;若满意度低于
,可抽奖2次;若满意度低于![]() ,可抽奖1次;②每次抽奖可获得的优惠券金额为10元或20元,相应的概率均为
,可抽奖1次;②每次抽奖可获得的优惠券金额为10元或20元,相应的概率均为![]() .求参与网络问卷调查的客户人均可获得优惠券金额(单位:元).
.求参与网络问卷调查的客户人均可获得优惠券金额(单位:元).
(附:参考数据与公式:若![]() ,则
,则![]() ,
,![]() ,
,![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥D-ABC中,![]() ,且
,且![]() ,
,![]() ,M,N分别是棱BC,CD的中点,下面结论正确的是( )
,M,N分别是棱BC,CD的中点,下面结论正确的是( )
A.![]() B.
B.![]() 平面ABD
平面ABD
C.三棱锥A-CMN的体积的最大值为![]() D.AD与BC一定不垂直
D.AD与BC一定不垂直
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com