
【题目】对于定义域为D的函数![]() ,若同时满足下列条件:①
,若同时满足下列条件:①![]() 在D内单调递增或单调递减;②存在区间
在D内单调递增或单调递减;②存在区间![]() ,使
,使![]() 在
在![]() 上的值域为
上的值域为![]() ,则把
,则把![]() 叫闭函数。
叫闭函数。
(1)求闭函数![]() 符合条件②的区间
符合条件②的区间![]() ;
;
(2)判断函数![]() 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)已知![]() 是正整数,且定义在
是正整数,且定义在![]() 的函数
的函数![]() 是闭函数,求正整数
是闭函数,求正整数![]() 的最小值,及此时实数k的取值范围。
的最小值,及此时实数k的取值范围。
【答案】(1)![]() ;(2)不是,理由见解析;(3)
;(2)不是,理由见解析;(3)![]() 。
。
【解析】
试题分析:(1)由题意,![]() 在
在![]() 上递减,在
上递减,在![]() 上的值域为
上的值域为![]() ,故有
,故有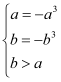 ,求得
,求得![]() 、
、![]() 的值,可得结论;(2)取
的值,可得结论;(2)取![]() ,则由
,则由![]() ,可得
,可得![]() 不是
不是![]() 上的减函数。同理求得
上的减函数。同理求得![]() 不是
不是![]() 上的增函数,从而该函数不是闭函数;(3)由题意,可得方程
上的增函数,从而该函数不是闭函数;(3)由题意,可得方程![]() 在
在![]() 上有两个不等的实根.利用基本不等式求得当
上有两个不等的实根.利用基本不等式求得当![]() 时,
时,![]() 取得最小值为
取得最小值为![]() .再根据函数
.再根据函数![]() 在
在![]() 上递减,在
上递减,在![]() 递增,而函数
递增,而函数![]() 与
与![]() 在
在![]() 有两个交点,可得正整数
有两个交点,可得正整数![]() 的最小值为
的最小值为![]() ,此时,
,此时,![]() ,由此求得
,由此求得![]() 的范围。
的范围。
试题解析:(1)由题意,![]() 在
在![]() 上递减,则
上递减,则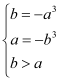 解得
解得![]() 所以,所求的区间为
所以,所求的区间为![]() 。
。
(2)取![]() 则
则![]() ,即
,即![]() 不是
不是![]() 上的减函数。取
上的减函数。取![]()
![]() ,即
,即![]() 不是
不是![]() 上的增函数。所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。
上的增函数。所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。
(3)![]() 是闭函数,则存在区间
是闭函数,则存在区间![]() ,使函数
,使函数![]() 的值域为
的值域为![]() ,
,![]() 在
在![]() 单调递增,即
单调递增,即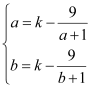 ,
,![]() 为方程
为方程![]() 的两个实根,即方程
的两个实根,即方程![]() 在
在![]() 上有两个不等的实根。
上有两个不等的实根。![]() ,当且仅当
,当且仅当![]() 时取等号考察函数
时取等号考察函数![]()
∵函数![]() 在
在![]() 上递减,∴
上递减,∴![]() 。
。
∵![]() 在
在![]() 递增,而函数
递增,而函数![]() 与
与![]() 在
在![]() 有两个交点。
有两个交点。
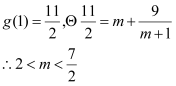
所以正整数![]() 的最小值为
的最小值为![]() ,
,![]() ,此时
,此时![]() 的取值范围为
的取值范围为![]() 。
。


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
【题目】下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是( )
A.f(x)=ln|x|
B.f(x)=2﹣x
C.f(x)=x3
D.f(x)=﹣x2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】比较下列各题中两个值的大小.
(1)1.82.2 , 1.83;
(2)0.7-0.3 , 0.7-0.4;
(3)1.90.4 , 0.92.4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A. 如果两条直线都平行于同一个平面,那么这两条直线互相平行
B. 过一条直线有且只有一个平面与已知平面垂直
C. 如果一条直线平行于一个平面内的一条直线,那么这条直线平行于这个平面
D. 如果两条直线都垂直于同一平面,那么这两条直线共面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月13日,中国郑开国际马拉松赛在郑东新区开赛.比赛之前,从某大学报名的30名大学生中选8人进行志愿者服务,请分别用抽签法和随机数法设计抽样方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一房产商竞标得一块扇形![]() 地皮,其圆心角
地皮,其圆心角![]()
![]() ,半径为
,半径为![]()
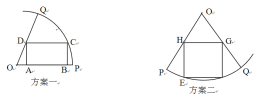
![]() ,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形
,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形![]() 的一边
的一边![]() 在半径
在半径![]() 上,
上,![]() 在圆弧上,
在圆弧上,![]() 在半径
在半径![]() ;方案二:矩形EFGH的顶点在圆弧上,顶点
;方案二:矩形EFGH的顶点在圆弧上,顶点![]() 分别在两条半径上。请你通过计算,为房产商提供决策建议。
分别在两条半径上。请你通过计算,为房产商提供决策建议。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知小矩形花坛ABCD中,AB=3m,AD=2m,现要将小矩形花坛建成大矩形花坛AMPN,使点B在AM上,点D在AN上,且对角线MN过点C.

(1)要使矩形AMPN的面积大于32m2,AN的长应在什么范围内?
(2)M,N是否存在这样的位置,使矩形AMPN的面积最小?若存在,求出这个最小面积及相应的AM。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装厂生产一种服装的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购超过100件时,每多订购1件,订购的全部服装的出场单价就降低0.02元,根据市场调查,销售商一次订购量不会超过600件.
(1)设销售一次订购![]() 件,服装的实际出厂单价为
件,服装的实际出厂单价为![]() 元,写出函数
元,写出函数![]() 的表达式;
的表达式;
(2)当销售商一次订购多少件服装时,该厂获得的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com