
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
| s |
| t |
| s |
| t |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
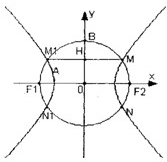 如图F1(-c,0),F2(c,0)为双曲线E的两焦点,以F1F2为直径的圆O与双曲线E交于M、N、M1、N1,B是圆O与y轴的交点,连接MM1与OB交于H,且H是OB的中点.
如图F1(-c,0),F2(c,0)为双曲线E的两焦点,以F1F2为直径的圆O与双曲线E交于M、N、M1、N1,B是圆O与y轴的交点,连接MM1与OB交于H,且H是OB的中点.| F1A |
| AM |
查看答案和解析>>
科目:高中数学 来源: 题型:
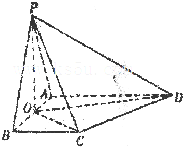 如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AD∥BC,∠ABC=90°,PA=PB=3,BC=1,AB=2,AD=3,O是AB中点.
如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AD∥BC,∠ABC=90°,PA=PB=3,BC=1,AB=2,AD=3,O是AB中点.| CM | PC |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省乐清市高三第一次月考理科数学试卷(解析版) 题型:解答题
已知△ABC中,角A、B、C的对边为a,b,c,向量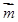
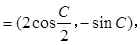
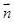 =
=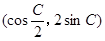 ,且
,且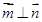 .
(1)求角C; (2)若
.
(1)求角C; (2)若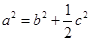 ,试求
,试求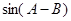 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市朝阳区高三3月第一次综合练习理科数学试卷(解析版) 题型:解答题
已知椭圆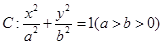 的两个焦点分别为
的两个焦点分别为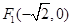 ,
,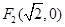 .点
.点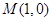 与椭圆短轴的两个端点的连线相互垂直.
与椭圆短轴的两个端点的连线相互垂直.
(Ⅰ)求椭圆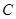 的方程;
的方程;
(Ⅱ)已知点 的坐标为
的坐标为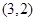 ,点
,点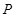 的坐标为
的坐标为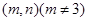 .过点
.过点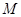 任作直线
任作直线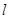 与椭圆
与椭圆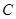 相交于
相交于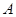 ,
,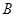 两点,设直线
两点,设直线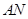 ,
,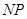 ,
,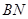 的斜率分别为
的斜率分别为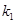 ,
, ,
,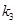 ,若
,若
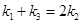 ,试求
,试求 满足的关系式.
满足的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com