
【题目】已知关于x的不等式(kx﹣k2﹣4)(x﹣4)>0,其中k∈R;
(1)当k=4时,求上述不等式的解集;
(2)当上述不等式的解集为(﹣5,4)时,求k的值.
【答案】
(1)解:关于x的不等式(kx﹣k2﹣4)(x﹣4)>0,
当k=4时,不等式化为(4x﹣16﹣4)(x﹣4)>0,
解得x<4或x>5,
所以不等式的解集为(﹣∞,4)∪(5,+∞);
(2)解:当不等式(kx﹣k2﹣4)(x﹣4)>0的解集为(﹣5,4)时,
有  ,
,
解得k=﹣1或k=﹣4.
【解析】(1)当k=4时,不等式化为(4x﹣16﹣4)(x﹣4)>0,求出解集即可,(2)不等式的解集为(﹣5,4)时,可得出一根为4,一根为-5,即可解得k的大小.
【考点精析】利用解一元二次不等式对题目进行判断即可得到答案,需要熟知求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(1﹣x)﹣ln(1+x),则f(x)是( )
A.奇函数,且在(0,1)上是增函数
B.奇函数,且在(0,1)上是减函数
C.偶函数,且在(0,1)上是增函数
D.偶函数,且在(0,1)上是减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂生产某种产品,当年产量在150吨至250吨时,每年的生产成本y万元与年产量x吨之间的关系可可近似地表示为y= ![]() ﹣30x+4000.
﹣30x+4000.
(1)若每年的生产总成本不超过2000万元,求年产量x的取值范围;
(2)求年产量为多少吨时,每吨的平均成本最低,并求每吨的最低成本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动. 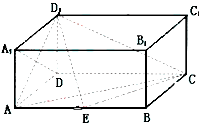
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1﹣EC﹣D的大小为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】非空集合G关于运算⊕满足:
⑴对任意a,b∈G,都有a+b∈G;
⑵存在e∈G使得对于一切a∈G都有a⊕e=e⊕a=a,
则称G是关于运算⊕的融洽集,
现有下列集合与运算:
①G是非负整数集,⊕:实数的加法;
②G是偶数集,⊕:实数的乘法;
③G是所有二次三项式构成的集合,⊕:多项式的乘法;
④G={x|x=a+b ![]() ,a,b∈Q},⊕:实数的乘法;
,a,b∈Q},⊕:实数的乘法;
其中属于融洽集的是(请填写编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长是2的正方体ABCD﹣A1B1C1D1中,E,F分别为AB,A1C的中点.应用空间向量方法求解下列问题. 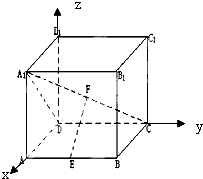
(1)求EF的长
(2)证明:EF∥平面AA1D1D;
(3)证明:EF⊥平面A1CD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com