
【题目】在一次招聘中,主考官要求应聘者从6道备选题中一次性随机抽取3道题,并独立完成所抽取的3道题。甲能正确完成其中的4道题,乙能正确完成每道题的概率为![]() ,且每道题完成与否互不影响。
,且每道题完成与否互不影响。
⑴记所抽取的3道题中,甲答对的题数为X,则X的分布列为____________;
⑵记乙能答对的题数为Y,则Y的期望为_________.
科目:高中数学 来源: 题型:
【题目】某中学高三年级有学生500人,其中男生300人,女生200人。为了研究学生的数学成绩是否与性别有关,采用分层抽样的方法,从中抽取了100名学生,统计了他们期中考试的数学分数,然后按照性别分为男、女两组,再将两组的分数分成5组: ![]() 分别加以统计,得到如图所示的频率分布直方图。
分别加以统计,得到如图所示的频率分布直方图。

(I)从样本分数小于110分的学生中随机抽取2人,求两人恰为一男一女的概率;
(II)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
 附表:
附表:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有![]() 五辆汽车,其中
五辆汽车,其中![]() 两辆汽车的车牌尾号均为1.
两辆汽车的车牌尾号均为1. ![]() 两辆汽车的车牌尾号均为2,
两辆汽车的车牌尾号均为2, ![]() 车的车牌尾号为6,已知在非限行日,每辆车可能出车或不出车,
车的车牌尾号为6,已知在非限行日,每辆车可能出车或不出车, ![]() 三辆汽车每天出车的概率均为
三辆汽车每天出车的概率均为![]() ,
, ![]() 两辆汽车每天出车的概率均为
两辆汽车每天出车的概率均为![]() ,且五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
,且五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
(1)求该公司在星期一至少有2辆汽车出国的概率;
(2)设![]() 表示该公司在星期二和星期三两天出车的车辆数之和,求
表示该公司在星期二和星期三两天出车的车辆数之和,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,
的焦点, ![]() 为抛物线
为抛物线![]() 上不同的两点,
上不同的两点, ![]() 分别是抛物线
分别是抛物线![]() 在点
在点![]() 、点
、点![]() 处的切线,
处的切线, ![]() 是
是![]() 的交点.
的交点.
(1)当直线![]() 经过焦点
经过焦点![]() 时,求证:点
时,求证:点![]() 在定直线上;
在定直线上;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() ,各局比赛结果相互独立.
,各局比赛结果相互独立.
(1)求甲在4局以内(含4局)赢得比赛的概率;
(2)记X为比赛决出胜负时的总局数,求X的分布列和均值(数学期望).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 内单调递减,在区间
内单调递减,在区间![]() 内单调递增,且
内单调递增,且![]() 在
在![]() 上有三个零点,1是其中一个零点.
上有三个零点,1是其中一个零点.
(1)求![]() 的取值范围;
的取值范围;
(2)若直线![]() 在曲线
在曲线![]() 的上方部分所对应的
的上方部分所对应的![]() 的集合为
的集合为![]() ,试求实数
,试求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三(1)班全体女生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图所示,据此解答如下问题:

(1)求高三(1)班全体女生的人数;
(2)求分数在[80,90)之间的女生人数,并计算频率分布直方图中[80,90)之间的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析女生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
如图,在阳马![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 为
为![]() 中点,点
中点,点![]() 在
在![]() 上,且
上,且![]() 平面
平面![]() ,连接
,连接![]() ,
, ![]() .
.
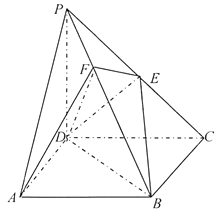
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)试判断四面体![]() 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
(Ⅲ)已知![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com