
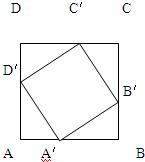
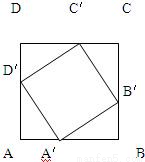
 已知ABCD,A'B'C'D'都是正方形(如图),而A'、B'、C'、D'分别把AB、BC、CD、DA分为m:n,设AB=1.
已知ABCD,A'B'C'D'都是正方形(如图),而A'、B'、C'、D'分别把AB、BC、CD、DA分为m:n,设AB=1.| 1 | 2 |
| 1 |
| m+n |
| m2+n2 |
| (m+n)2 |
| 1 |
| 2 |
| (m-n)2 |
| 2(m+n)2 |
| 1 |
| 2 |
| 1 |
| m+n |
| m2+n2 |
| (m+n)2 |
| m2+n2 |
| (m+n)2 |
| 1 |
| 2 |
| 2(m2+n2)-(m+n)2 |
| 2(m+n)2 |
| (m-n)2 |
| 2(m+n)2 |
| m2+n2 |
| (m+n)2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:高中数学 来源: 题型:
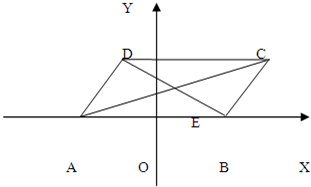 已知□ABCD,A(-2,0),B(2,0),且|AD|=2
已知□ABCD,A(-2,0),B(2,0),且|AD|=2| 8 |
| 3 |
| 2 |
| 4 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:新课标高三数学空间向量及其运算、角的概念及其求法和空间距离专项训练(河北) 题型:解答题
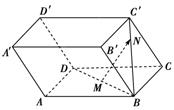
已知ABCD-A′B′C′D′是平行六面体.
(1)化简++,并在图形中标出其结果;
(2)设M是底面ABCD的中心,N是侧面BCC′B′的对角线BC′上的点,且BN∶NC′=3∶1,设=α+β+γ,试求α,β,γ之值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
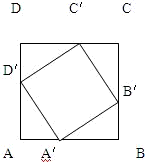 已知ABCD,A'B'C'D'都是正方形(如图),而A'、B'、C'、D'分别把AB、BC、CD、DA分为m:n,设AB=1.
已知ABCD,A'B'C'D'都是正方形(如图),而A'、B'、C'、D'分别把AB、BC、CD、DA分为m:n,设AB=1. .
.查看答案和解析>>
科目:高中数学 来源:1962年全国统一高考数学试卷(解析版) 题型:解答题
 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com