
 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面 ABCD,且PA=AD=DB=$\frac{1}{2}$,AB=1,M是PB的中点.
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面 ABCD,且PA=AD=DB=$\frac{1}{2}$,AB=1,M是PB的中点.分析 (1)由三垂线定理得CD⊥PD,从而CD⊥面PAD,再由CD?面PCD,能证明面PAD⊥面PCD.
(2)过点B作BE∥CA,且BE=CA,则∠PBE是AC与PB所成的角. 连接AE,推导出四边形ACBE为正方形,由此能求出AC与PB所成的角.
(3)作AN⊥CM,垂足为N,连接BN,则∠ANB为所求二面角的平面角,由此能求出平面AMC与平面BMC所成二面角的大小.
解答 证明:(1)∵PA⊥面ABCD,CD⊥AD,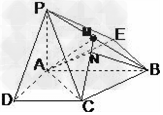
∴由三垂线定理得:CD⊥PD.
因而,CD与面PAD内两条相交直线AD,PD都垂直,
∴CD⊥面PAD.
又CD?面PCD,∴面PAD⊥面PCD.
解:(2)过点B作BE∥CA,且BE=CA,则∠PBE是AC与PB所成的角.
连接AE,可知AC=CB=BE=AE=$\sqrt{2}$,
又AB=2,所以四边形ACBE为正方形.
由PA⊥面ABCD,得∠PEB=90°
在Rt△PEB中,BE=a2=3b2,PB=$\sqrt{5}$,
∴cos∠PBE=$\frac{BE}{PB}$=$\frac{\sqrt{10}}{5}$.
∴AC与PB所成的角为arccos$\frac{\sqrt{10}}{5}$.
(3)作AN⊥CM,垂足为N,连接BN.
在Rt△PAB中,AM=MB,又AC=CB,
∴△AMC≌△BMC,
∴BN⊥CM,故∠ANB为所求二面角的平面角
∵CB⊥AC,
由三垂线定理,得CB⊥PC,
在Rt△PCB中,CM=MB,所以CM=AM.
在等腰三角形AMC中,AN•MC=$\sqrt{C{M}^{2}-(\frac{AC}{2})^{2}}$•AC,
∴AN=$\frac{\frac{\sqrt{3}}{2}×\sqrt{2}}{\frac{\sqrt{5}}{2}}=\frac{\sqrt{6}}{\sqrt{5}}$.∴AB=2,
∴cos∠ANB=$\frac{A{N}^{2}+B{N}^{2}-A{B}^{2}}{2×AN×BN}$=-$\frac{2}{3}$,
故平面AMC与平面BMC所成二面角的大小为arccos(-$\frac{2}{3}$).
点评 本题考查面面垂直的证明,考百线线角的求法,考百二面角的大小的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在某校趣味运动会的颁奖仪式上,为了活跃气氛,大会组委会决定在颁奖过程中进行抽奖活动,用分层抽样的方法从参加颁奖仪式的高一、高二、高三代表队中抽取20人前排就座,其中高二代表队有6人.
在某校趣味运动会的颁奖仪式上,为了活跃气氛,大会组委会决定在颁奖过程中进行抽奖活动,用分层抽样的方法从参加颁奖仪式的高一、高二、高三代表队中抽取20人前排就座,其中高二代表队有6人.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{5}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{11}$ | B. | $\frac{3}{11}$ | C. | $\frac{6}{11}$ | D. | $\frac{5}{11}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com