
°æƒø°ø‘⁄2018ƒÍ3‘¬÷£÷ðµ⁄∂˛¥Œƒ£ƒ‚øº ‘÷–£¨ƒ≥–£π≤”–100√˚Œƒø∆—ß…˙≤Œº”øº ‘£¨∆‰÷–”ÔŒƒøº ‘≥…º®µÕ”⁄130µƒ’º95%»À£¨ ˝—ß≥…º®µƒ∆µ¬ ∑÷≤º÷±∑ΩÕº»ÁÕº£∫
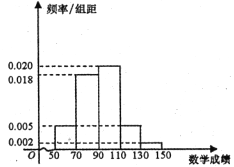
£®¢Ò£©»Áπ˚≥…º®≤ªµÕ”⁄130µƒŒ™Ãÿ±”≈–„£¨’‚100√˚—ß…˙÷–±æ¥Œøº ‘”ÔŒƒ°¢ ˝—ß≥…º®Ãÿ±”≈–„µƒ¥Û‘º∏˜∂ý…Ÿ»À£ø
£®¢Ú£©»Áπ˚”ÔŒƒ∫Õ ˝—ß¡Ωø∆∂ºÃÿ±”≈–„µƒπ≤”–3»À£Æ
£®¢°£©¥”£®¢Ò£©÷–µƒ’‚–©Õ¨—ß÷–Àʪ˙≥È»°2»À£¨«Û’‚¡Ω»À¡Ωø∆≥…º®∂º”≈–„µƒ∏≈¬ £Æ
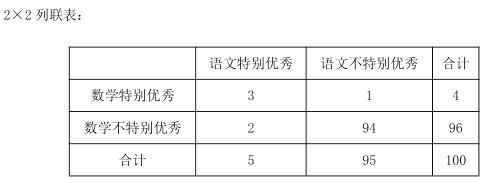
£®¢¢£©∏˘æð“‘…œ ˝æð£¨ÕÍ≥…![]() ¡–¡™±Ì£¨≤¢∑÷Œˆ «∑Ò”–99%µƒ∞—Œ’»œŒ™”ÔŒƒÃÿ±”≈–„µƒÕ¨—ߣ¨ ˝—ß“≤Ãÿ±”≈–„£Æ
¡–¡™±Ì£¨≤¢∑÷Œˆ «∑Ò”–99%µƒ∞—Œ’»œŒ™”ÔŒƒÃÿ±”≈–„µƒÕ¨—ߣ¨ ˝—ß“≤Ãÿ±”≈–„£Æ
”ÔŒƒÃÿ±”≈–„ | ”ÔŒƒ≤ªÃÿ±”≈–„ | ∫œº∆ | |
˝—ßÃÿ±”≈–„ | |||
˝—ß≤ªÃÿ±”≈–„ | |||
∫œº∆ |
![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
°æ¥∞∏°ø£®¢Ò£©![]() £ª£®¢Ú£©(i)
£ª£®¢Ú£©(i)![]() £¨£®ii£©”–∞—Œ’.
£¨£®ii£©”–∞—Œ’.
°æΩ‚Œˆ°ø∑÷Œˆ£∫£®1£©”…∆µ¬ ∑÷≤º÷±∑ΩÕº«Û≥ˆ≥…º®≤ªµÕ”⁄130µƒ∏≈¬ £¨Ω¯∂¯µ√µΩ«ÛΩ‚£¨
£®2£©¡–æŸ≥ˆÀ˘”–ª˘±æ ¬º˛£¨
£®3£©∏˘æðº∆À„ ˝æð¡–≥ˆ¡–¡™±Ì£¨º∆À„≥ˆ![]() £¨≤ȱÌø…µ√°£
£¨≤ȱÌø…µ√°£
œÍΩ‚£∫£®¢Ò£©Œ“–£π≤”–100√˚Œƒø∆—ß…˙≤Œº”øº ‘£¨∆‰÷–”ÔŒƒøº ‘≥…º®µÕ”⁄130µƒ”–95%»À£¨”ÔŒƒ≥…º®Ãÿ±”≈–„µƒ∏≈¬ Œ™![]() £¨”ÔŒƒÃÿ±”≈–„µƒÕ¨—ß”–
£¨”ÔŒƒÃÿ±”≈–„µƒÕ¨—ß”–![]() »À£¨ ˝—ß≥…º®Ãÿ±”≈–„µƒ∏≈¬ Œ™
»À£¨ ˝—ß≥…º®Ãÿ±”≈–„µƒ∏≈¬ Œ™![]() £¨ ˝—ßÃÿ±”≈–„µƒÕ¨—ß”–
£¨ ˝—ßÃÿ±”≈–„µƒÕ¨—ß”–![]() »À£ª
»À£ª
£®¢Ú£©(i)”ÔŒƒ ˝—ß¡Ωø∆∂º”≈–„µƒ”–3»À£¨µ•ø∆”≈–„µƒ”–3»À£¨
º«¡Ωø∆∂º”≈–„µƒ3»À∑÷±Œ™![]() £¨µ•ø∆”≈–„µƒ3»À∑÷±Œ™
£¨µ•ø∆”≈–„µƒ3»À∑÷±Œ™![]() £¨¥”÷–Àʪ˙≥È»°2»À£¨π≤”–£∫
£¨¥”÷–Àʪ˙≥È»°2»À£¨π≤”–£∫![]() £¨
£¨![]() £¨
£¨![]()
![]()
![]() π≤15÷÷£¨∆‰÷–’‚¡Ω»À≥…º®∂º”≈–„µƒ”–
π≤15÷÷£¨∆‰÷–’‚¡Ω»À≥…º®∂º”≈–„µƒ”–![]() 3÷÷£¨‘Ú’‚¡Ω»À¡Ωø∆≥…º®∂º”≈–„µƒ∏≈¬ Œ™£∫
3÷÷£¨‘Ú’‚¡Ω»À¡Ωø∆≥…º®∂º”≈–„µƒ∏≈¬ Œ™£∫![]() £ª
£ª
£®ii£©
![]()
![]() ”–95%µƒ∞—Œ’»œŒ™”ÔŒƒÃÿ±”≈–„µƒÕ¨—ߣ¨ ˝—ß“≤Ãÿ±”≈–„£Æ
”–95%µƒ∞—Œ’»œŒ™”ÔŒƒÃÿ±”≈–„µƒÕ¨—ߣ¨ ˝—ß“≤Ãÿ±”≈–„£Æ


 ∆þ≤ Âø®ø⁄À„”¶”√“ªµ„Õ®œµ¡–¥∞∏
∆þ≤ Âø®ø⁄À„”¶”√“ªµ„Õ®œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤![]() µƒ¿Î–ƒ¬ Œ™
µƒ¿Î–ƒ¬ Œ™![]() £¨µ„
£¨µ„![]() Œ™Õ÷‘≤…œ“ªµ„.
Œ™Õ÷‘≤…œ“ªµ„.
£®1£©«ÛÕ÷‘≤Cµƒ∑Ω≥ãª
£®2£©“—÷™¡ΩÃıª•œý¥π÷±µƒ÷±œþ![]() £¨
£¨![]() æ≠π˝Õ÷‘≤
æ≠π˝Õ÷‘≤![]() µƒ”“Ωπµ„
µƒ”“Ωπµ„![]() £¨”ÎÕ÷‘≤
£¨”ÎÕ÷‘≤![]() Ωª”⁄
Ωª”⁄![]() Àƒµ„£¨«ÛÀƒ±þ–Œ
Àƒµ„£¨«ÛÀƒ±þ–Œ![]() √ʪ˝µƒµƒ»°÷µ∑∂Œß.
√ʪ˝µƒµƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥°∞≈©º“¿÷°±Ω”¥˝÷––ƒ”–øÕ∑ø200º‰£¨√øº‰»’◊‚ΩŒ™40‘™£¨√øÃÏ∂ºøÕ¬˙.∏˘æ𠵺 –Ë“™£¨∏√÷––ƒ–Ë÷∏þ◊‚Ω£¨»Áπ˚√øº‰øÕ∑ø»’◊‚Ω√ø‘ˆº”4‘™£¨øÕ∑ø≥ˆ◊‚æÕª·ºı…Ÿ10º‰.£®≤ªøº¬«∆‰À˚“ÚÀÿ£©
£®1£©…Ë√øº‰øÕ∑ø»’◊‚Ω÷∏þ![]() ‘™£®
‘™£®![]() £©£¨º«∏√÷––ƒøÕ∑øµƒ»’◊‚Ω◊Ð ’»ÎŒ™
£©£¨º«∏√÷––ƒøÕ∑øµƒ»’◊‚Ω◊Ð ’»ÎŒ™![]() £¨ ‘”√
£¨ ‘”√![]() ±Ì æ
±Ì æ![]()
£®2£©‘⁄£®1£©µƒÃıº˛œ¬£¨√øº‰øÕ∑ø»’◊‚ΩŒ™∂ý…Ÿ ±£¨∏√÷––ƒøÕ∑øµƒ»’◊‚Ω◊Ð ’»Î◊Ó∏þ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄µÿ√Ê…œÕ¨“ªµÿµ„π€≤‚‘∂∑Ω‘»ÀŸ¥π÷±…œ…˝µƒ»»∆¯«Ú£¨‘⁄…œŒÁ10µ„’˚»»∆¯«Úµƒ—ˆΩ« «![]() £¨µΩ…œŒÁ10µ„20∑÷µƒ—ˆΩ«±‰≥…
£¨µΩ…œŒÁ10µ„20∑÷µƒ—ˆΩ«±‰≥…![]() .«Î¿˚”√œ¬±Ì≈–∂œµΩ…œŒÁ11µ„’˚ ±£¨»»∆¯«Úµƒ—ˆΩ«◊ÓΩ”Ω¸ƒƒ∏ˆ∂» ˝( )
.«Î¿˚”√œ¬±Ì≈–∂œµΩ…œŒÁ11µ„’˚ ±£¨»»∆¯«Úµƒ—ˆΩ«◊ÓΩ”Ω¸ƒƒ∏ˆ∂» ˝( )
|
|
|
|
|
|
|
|
|
|
| 0.5 | 0.559 | 0.629 | 0.643 | 0.656 | 0.669 | 0.682 | 0.695 | 0.707 |
| 0.866 | 0.829 | 0.777 | 0.766 | 0.755 | 0.743 | 0.731 | 0.719 | 0.707 |
| 0.577 | 0.675 | 0.810 | 0.839 | 0.869 | 0.900 | 0.933 | 0.966 | 1.0 |
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™”≠Ω”œƒºæ¬√”ŒÕ˙ºæµƒµΩ¿¥£¨…Ÿ¡÷À¬µ•∂¿…Ë÷√¡À“ª∏ˆ◊®√≈∞≤≈≈”ŒøÕ◊°ÀÞµƒøÕ’ª£¨À¬√̵ƒπ§◊˜»À‘±∑¢œ÷Œ™”ŒøÕ◊º±∏µƒ“ª–© ≥ŒÔ”––©‘¬∑ð £”ý≤ª…Ÿ£¨¿À∑—∫Зœ÷ÿ£¨Œ™¡Àøÿ÷∆æ≠”™≥…±æ£¨ºı…Ÿ¿À∑—£¨æ՜Π±µ˜’˚Õ∂»Î£ÆŒ™¥ÀÀ˚√«Õ≥º∆√ø∏ˆ‘¬»Î◊°µƒ”ŒøÕ»À ˝£¨∑¢œ÷√øƒÍ∏˜∏ˆ‘¬∑ð¿¥øÕ’ª»Î◊°µƒ”ŒøÕ»À ˝ª·∑¢…˙÷Ð∆⁄–‘µƒ±‰ªØ£¨≤¢«“”–“‘œ¬πʬ…£∫
¢Ÿ√øƒÍœýÕ¨µƒ‘¬∑𣨻Î◊°øÕ’ªµƒ”ŒøÕ»À ˝ª˘±æœýÕ¨£ª
¢⁄»Î◊°øÕ’ªµƒ”ŒøÕ»À ˝‘⁄2‘¬∑ð◊Ó…Ÿ£¨‘⁄8‘¬∑ð◊Ó∂ý£¨œý≤Ó‘º400»À£ª
¢€2‘¬∑ð»Î◊°øÕ’ªµƒ”ŒøÕ‘ºŒ™100»À£¨ÀÊ∫Û÷‘¬µð‘ˆ÷±µΩ8‘¬∑ð¥ÔµΩ◊Ó∂ý£Æ
£®1£© ‘”√“ª∏ˆ’˝œ“–Õ»˝Ω«∫Ø ˝![]() √Ë ˆ“ªƒÍ÷–»Î◊°øÕ’ªµƒ”ŒøÕ»À ˝y”Α¬x∑ð÷ƺ‰µƒπÿœµ£ª
√Ë ˆ“ªƒÍ÷–»Î◊°øÕ’ªµƒ”ŒøÕ»À ˝y”Α¬x∑ð÷ƺ‰µƒπÿœµ£ª
£®2£©«ÎŒ ƒƒº∏∏ˆ‘¬∑ð“™◊º±∏400∑ð“‘…œµƒ ≥ŒÔ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
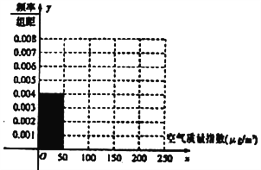
°æƒø°ø»´ ¿ΩÁ‘Ω¿¥‘Ωπÿ◊¢ª∑æ≥±£ª§Œ £¨ƒ≥ºý≤‚’浄”⁄2018ƒÍ1‘¬ƒ≥»’∆¡¨–¯![]() ÃϺý≤‚ø’∆¯÷ ¡ø÷∏ ˝(
ÃϺý≤‚ø’∆¯÷ ¡ø÷∏ ˝(![]() )£¨ ˝æðÕ≥º∆»Áœ¬£∫
)£¨ ˝æðÕ≥º∆»Áœ¬£∫
ø’∆¯÷ ¡ø÷∏ ˝( |
|
|
|
|
|
ø’∆¯÷ ¡øµ»º∂ | ø’∆¯”≈ | ø’∆¯¡º | «·∂»Œ€»æ | ÷–∂»Œ€»æ | ÷ÿ∂»Œ€»æ |
ÃÏ ˝ | 20 | 40 |
| 10 | 5 |
£®1£©∏˘æðÀ˘∏¯Õ≥º∆±Ì∫Õ∆µ¬ ∑÷≤º÷±∑ΩÕº÷–µƒ–≈œ¢«Û≥ˆ![]() £¨
£¨![]() µƒ÷µ£¨≤¢ÕÍ≥…∆µ¬ ∑÷≤º÷±∑ΩÕº£ª
µƒ÷µ£¨≤¢ÕÍ≥…∆µ¬ ∑÷≤º÷±∑ΩÕº£ª
£®2£©”…∆µ¬ ∑÷≤º÷±∑ΩÕº£¨«Û∏√◊È ˝æðµƒ÷⁄ ˝∫Õ÷–Œª ˝£ª
£®3£©‘⁄ø’∆¯÷ ¡ø÷∏ ˝∑÷± Ù”⁄![]() ∫Õ
∫Õ![]() µƒºý≤‚ ˝æð÷–£¨”√∑÷≤„≥È—˘µƒ∑Ω∑®≥È»°
µƒºý≤‚ ˝æð÷–£¨”√∑÷≤„≥È—˘µƒ∑Ω∑®≥È»°![]() ÃÏ£¨‘Ÿ¥”÷–»Œ“‚—°»°
ÃÏ£¨‘Ÿ¥”÷–»Œ“‚—°»°![]() ÃÏ£¨«Û ¬º˛
ÃÏ£¨«Û ¬º˛![]() °∞¡ΩÃÏø’∆¯∂ºŒ™¡º°±∑¢…˙µƒ∏≈¬ .
°∞¡ΩÃÏø’∆¯∂ºŒ™¡º°±∑¢…˙µƒ∏≈¬ .
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂®“‘⁄£®0£¨+°Þ£©…œµƒ∫Ø ˝f£®x£©µƒµº ˝![]() ¬˙◊„x2
¬˙◊„x2![]() £º1£¨‘Úœ¬¡–≤ªµ» Ω÷–“ª∂®≥…¡¢µƒ «£®°°°°£©
£º1£¨‘Úœ¬¡–≤ªµ» Ω÷–“ª∂®≥…¡¢µƒ «£®°°°°£©
A.f£®![]() £©+1£ºf£®
£©+1£ºf£®![]() £©£ºf£®
£©£ºf£®![]() £©©Å1B.f£®
£©©Å1B.f£®![]() £©+1£ºf£®
£©+1£ºf£®![]() £©£ºf£®
£©£ºf£®![]() £©©Å1
£©©Å1
C.f£®![]() £©©Å1£ºf£®
£©©Å1£ºf£®![]() £©£ºf£®
£©£ºf£®![]() £©+1D.f£®
£©+1D.f£®![]() £©©Å1£ºf£®
£©©Å1£ºf£®![]() £©£ºf£®
£©£ºf£®![]() £©+1
£©+1
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©£Ωalnx©Åex£®a° R£©£Æ∆‰÷–e «◊‘»ª∂‘ ˝µƒµ◊ ˝£Æ
£®1£©Ã÷¬€∫Ø ˝f£®x£©µƒµ•µ˜–‘≤¢«Ûº´÷µ£ª
£®2£©¡Ó∫Ø ˝g£®x£©£Ωf£®x£©+ex£¨»Ùx° [1£¨+°Þ£© ±£¨g£®x£©°ð0£¨«Û µ ˝aµƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨µ„![]() ∑÷± «‘≤–ƒ‘⁄‘≠µ„£¨∞Îæ∂Œ™
∑÷± «‘≤–ƒ‘⁄‘≠µ„£¨∞Îæ∂Œ™![]() ∫Õ
∫Õ![]() µƒ‘≤…œµƒ∂ص„.∂ص„
µƒ‘≤…œµƒ∂ص„.∂ص„![]() ¥”≥ı ºŒª÷√
¥”≥ı ºŒª÷√![]() ø™ º£¨∞¥ƒÊ ±’Î∑ΩœÚ“‘Ω«ÀŸ∂»
ø™ º£¨∞¥ƒÊ ±’Î∑ΩœÚ“‘Ω«ÀŸ∂»![]() ◊˜‘≤÷БÀ∂Ø£¨Õ¨ ±µ„
◊˜‘≤÷БÀ∂Ø£¨Õ¨ ±µ„![]() ¥”≥ı ºŒª÷√
¥”≥ı ºŒª÷√![]() ø™ º£¨∞¥À≥ ±’Î∑ΩœÚ“‘Ω«ÀŸ∂»
ø™ º£¨∞¥À≥ ±’Î∑ΩœÚ“‘Ω«ÀŸ∂»![]() ◊˜‘≤÷БÀ∂Ø.º«
◊˜‘≤÷БÀ∂Ø.º«![]() ±ø㨵„
±ø㨵„![]() µƒ◊ð◊¯±Í∑÷±Œ™
µƒ◊ð◊¯±Í∑÷±Œ™![]() .
.
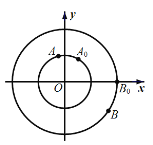
£®¢Ò£©«Û![]() ±øã¨
±øã¨![]() ¡Ωµ„º‰µƒæý¿Î£ª
¡Ωµ„º‰µƒæý¿Î£ª
£®¢Ú£©«Û![]() πÿ”⁄ ±º‰
πÿ”⁄ ±º‰![]() µƒ∫Ø ˝πÿœµ Ω£¨≤¢«Ûµ±
µƒ∫Ø ˝πÿœµ Ω£¨≤¢«Ûµ±![]() ±£¨’‚∏ˆ∫Ø ˝µƒ÷µ”Ú.
±£¨’‚∏ˆ∫Ø ˝µƒ÷µ”Ú.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com