
【题目】已知四棱锥![]() ,
,![]() ,在平行四边形
,在平行四边形![]() 中,
中,![]() ,Q为
,Q为![]() 上的点,过
上的点,过![]() 的平面分别交
的平面分别交![]() ,
,![]() 于点E、F,且
于点E、F,且![]() 平面
平面![]() .
.
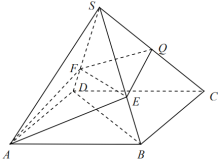
(1)证明:![]() ;
;
(2)若![]() ,
,![]() ,Q为
,Q为![]() 的中点,
的中点,![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)利用线面平行的性质可知![]() ,再后再根据条件证明
,再后再根据条件证明![]() 平面
平面![]() ,从而证明线线垂直;
,从而证明线线垂直;
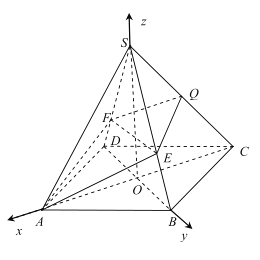
(2)如图,以O为坐标原点,分别以![]() 为
为![]() 轴建立空间直角坐标系,利用两个平面法向量求二面角的余弦值.
轴建立空间直角坐标系,利用两个平面法向量求二面角的余弦值.
(1)证明:连结![]() 交
交![]() 于点O,连结
于点O,连结![]() .
.
∵在平行四边形![]() 中,
中,![]() ,
,
∴![]() ,且O为
,且O为![]() 、
、![]() 的中点,
的中点,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,且
,且![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]()
∴![]() ,
,
∴![]()
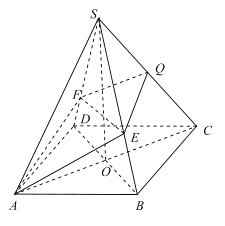
(2)由(1)可知![]() 平面
平面![]() ,故平面
,故平面![]() 平面
平面![]()
∵![]() ,且O为
,且O为![]() 的中点,∴
的中点,∴![]()
又∵平面![]() 平面
平面![]()
∴![]() 平面
平面![]() ,
,
∴![]() 与平面
与平面![]() 所成角为
所成角为![]()
∵![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,且
,且![]() ,∴
,∴![]() ,
,![]()
在![]() 中,
中,![]() ,由勾股定理得:
,由勾股定理得:![]()
如图,以O为坐标原点,分别以![]() 为
为![]() 轴建立空间直角坐标系,则:
轴建立空间直角坐标系,则:
![]() ,
,
∵Q为![]() 的中点,∴
的中点,∴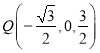
则![]() ,
,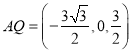
易知,平面![]() 的一个法向量为
的一个法向量为![]()
设平面![]() 的法向量为
的法向量为![]() ,因为
,因为![]() ,则:
,则:
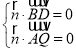 ,即
,即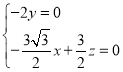 ,
,
令![]() ,则:
,则:![]() ,
,![]() ,故可取平面
,故可取平面![]() 的一个法向量为
的一个法向量为![]()
∴![]()
∴平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]()


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】某公司订购了一批树苗,为了检测这批树苗是否合格,从中随机抽测![]() 株树苗的高度,经数据处理得到如图1所示的频率分布直方图,其中最高的
株树苗的高度,经数据处理得到如图1所示的频率分布直方图,其中最高的![]() 株树苗的高度的茎叶图如图2所示,以这
株树苗的高度的茎叶图如图2所示,以这![]() 株树苗的高度的频率估计整批树苗高度的概率.
株树苗的高度的频率估计整批树苗高度的概率.
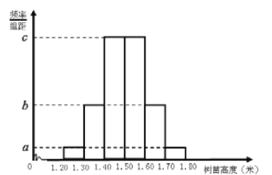

(1)求这批树苗的高度于![]() 米的概率,并求图
米的概率,并求图![]() 中
中![]() 的值;
的值;
(2)若从这批树苗中随机选取![]() 株,记
株,记![]() 为高度在
为高度在![]() 的树苗数量,求
的树苗数量,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若变量![]() 满足
满足![]() 且
且![]() ,则称变量
,则称变量![]() 满足近似于正态分布
满足近似于正态分布![]() 的概率分布,如果这批树苗的高度近似于正态分布
的概率分布,如果这批树苗的高度近似于正态分布![]() 的概率分布,则认为这批树苗是合格的,将顺利被签收,否则,公司将拒绝签收.试问:该批树苗是否被签收?
的概率分布,则认为这批树苗是合格的,将顺利被签收,否则,公司将拒绝签收.试问:该批树苗是否被签收?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年7月1日到3日,世界新能源汽车大会在海南博鳌召开,大会着眼于全球汽车产业的转型升级和生态环境的持续改善.某汽车公司顺应时代潮流,最新研发了一款新能源汽车,并在出厂前对100辆汽车进行了单次最大续航里程(理论上是指新能源汽车所装载的燃料或电池所能够提供给车行驶的最远里程)的测试.现对测试数据进行分析,得到如图的频率分布直方图.

(1)估计这100辆汽车的单次最大续航里程的平均值![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)根据大量的汽车测试数据,可以认为这款汽车的单次最大续航量程X近似地服从正态分布![]() ,经计算第(1)问中样本标准差s的近似值为50.用样本平均数
,经计算第(1)问中样本标准差s的近似值为50.用样本平均数![]() 作为
作为![]() 的近似值,用样本标准差s作为
的近似值,用样本标准差s作为![]() 的估计值,现任取一辆汽车,求它的单次最大续航里程恰在250千米到400千米之间的概率;
的估计值,现任取一辆汽车,求它的单次最大续航里程恰在250千米到400千米之间的概率;
(3)某汽车销售公司为推广此款新能源汽车,现面向意向客户推出“玩游戏,送大奖”活动,客户可根据抛掷硬币的结果,操控微型遥控车在方格图上行进,若遥控车最终停在“胜利大本营”,则可获得购车优惠券.已知硬币出现正,反面的概率都是![]() ,方格图上标有第0格、第1格、第2格……第50格.遥控车开始在第0格,客户每掷一次硬币,遥控车向前移动一次,若掷出正面,遥控车向前移动一格(从k到
,方格图上标有第0格、第1格、第2格……第50格.遥控车开始在第0格,客户每掷一次硬币,遥控车向前移动一次,若掷出正面,遥控车向前移动一格(从k到![]() ),若掷出反面,遥控车向前移动两格(从k到
),若掷出反面,遥控车向前移动两格(从k到![]() ),直到遥控车移到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束.设遥控车移到第n格的概率为
),直到遥控车移到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束.设遥控车移到第n格的概率为![]() ,试证明
,试证明![]() 是等比数列,并解释此方案能否成功吸引顾客购买该款新能源汽车.
是等比数列,并解释此方案能否成功吸引顾客购买该款新能源汽车.
参考数据:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为抗击新型冠状病毒,普及防护知识,某校开展了“疫情防护”网络知识竞赛活动.现从参加该活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
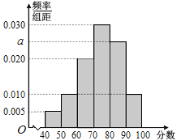
(1)求![]() 的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(2)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型公司为了切实保障员工的健康安全,贯彻好卫生防疫工作的相关要求,决定在全公司范围内举行一次乙肝普查.为此需要抽验669人的血样进行化验,由于人数较多,检疫部门制定了下列两种可供选择的方案.
方案一:将每个人的血分别化验,这时需要验669次.
方案二:按![]() 个人一组进行随机分组,把从每组
个人一组进行随机分组,把从每组![]() 个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这
个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这![]() 个人的血就只需检验一次(这时认为每个人的血化验
个人的血就只需检验一次(这时认为每个人的血化验![]() 次);否则,若呈阳性,则需对这
次);否则,若呈阳性,则需对这![]() 个人的血样再分别进行一次化验,这时该组
个人的血样再分别进行一次化验,这时该组![]() 个人的血总共需要化验
个人的血总共需要化验![]() 次.
次.
假设此次普查中每个人的血样化验呈阳性的概率为![]() ,且这些人之间的试验反应相互独立.
,且这些人之间的试验反应相互独立.
(1)设方案二中,某组![]() 个人中每个人的血化验次数为
个人中每个人的血化验次数为![]() ,求
,求![]() 的分布列.
的分布列.
(2)设![]() ,试比较方案二中,
,试比较方案二中,![]() 分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案一,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案一,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有大小、形状完全相同的四个小球,分别写有“和”、“谐”、“校”、“园”四个字,有放回地从中任意摸出一个小球,直到“和”、“谐”两个字都摸到就停止摸球,用随机模拟的方法估计恰好在第三次停止摸球的概率。利用电脑随机产生![]() 到
到![]() 之间取整数值的随机数,分别用
之间取整数值的随机数,分别用![]() ,
,![]() ,
,![]() ,
,![]() 代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下
代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下![]() 组随机数:
组随机数:
![]()
由此可以估计,恰好第三次就停止摸球的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着“一带一路”倡议的推进,中国与沿线国家旅游合作越来越密切,中国到“一带一路”沿线国家的游客人也越来越多,如图是2013-2018年中国到“一带一路”沿线国家的游客人次情况,则下列说法正确的是( )
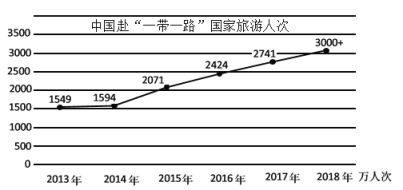
①2013-2018年中国到“一带一路”沿线国家的游客人次逐年增加
②2013-2018年这6年中,2014年中国到“一带一路”沿线国家的游客人次增幅最小
③2016-2018年这3年中,中国到“一带一路”沿线国家的游客人次每年的增幅基本持平
A.①②③B.②③C.①②D.③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() ,直线的参数方程为
,直线的参数方程为![]() ,(
,(![]() 为参数).直线
为参数).直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程.
的普通方程.
(2)设![]() ,若
,若![]() 成等比数列,求
成等比数列,求![]() 和的
和的![]() 值.
值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com