练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某人要利用无人机测量河流的宽度，如图，从无人机A处测得正前方河流的两岸B，C的俯角分别为75°，30°，此时无人机的高是60米，则河流的宽度BC等于（ ）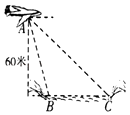

    A. 米
    B. 米
    C. 米
    D. 米

    【答案】C
    【解析】解：如图
    由图可知，∠DAB=15°，
    ∵tan15°=tan（45°﹣30°）=2﹣ ．
    在Rt△ADB中，又AD=60，
    ∴DB=ADtan15°=60×（2﹣ ）=120﹣60 ．
    在Rt△ADC中，∠DAC=60°，AD=60，
    ∴DC=ADtan60°=60 ．
    ∴BC=DC﹣DB=60 ﹣（120﹣60 ）=120（ ﹣1）（m）．
    ∴河流的宽度BC等于120（ ﹣1）m．
    故选：C．
    由题意画出图形，由两角差的正切求出15°的正切值，然后通过求解两个直角三角形得到DC和DB的长度，作差后可得答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在我国古代著名的数学专著《九章算术》里有﹣段叙述：今有良马与驽马发长安至齐，齐去长安一千一百二十五里，良马初日行一百零三里，日增十三里：驽马初日行九十七里，日减半里，良马先至齐，复还迎驽马，二马相逢，问：需日相逢．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直三棱柱ABC﹣A1B1C1中，AB⊥AC，AB=AC=2，A1A=4，点D是BC的中点；
    （I）求异面直线A1B，AC1所成角的余弦值；
    （II）求直线AB1与平面C1AD所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P﹣ABCD的底面ABCD是正方形，PA⊥平面ABCD，PA=AB=2．

    （1）若E，F分别是PC，AD的中点，证明：EF∥平面PAB；
    （2）若E是PC的中点，F是AD上的动点，问AF为何值时，EF⊥平面PBC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】比较下列各组数中两个数的大小．
    （1） 与 ；
    （2）3 与3.1 ；
    （3） 与 ；
    （4）0.20.6与0.30.4.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2x﹣ ． （Ⅰ）若f（x）=2，求x的值；
    （Ⅱ）若2tf（2t）+mf（t）≥0对于t∈[1，2]恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数f（x）=ax2+2x+c的对称轴为x=1，g（x）=x+ （x＞0）．
    （1）求函数g（x）的最小值及取得最小值时x的值；
    （2）试确定c的取值范围，使g（x）﹣f（x）=0至少有一个实根；
    （3）若F（x）=﹣f（x）+4x+c，存在实数t，对任意x∈[1，m]，使F（x+t）≤3x恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数f（x）满足f（x+1）﹣f（x）=2x（x∈R），且f（0）=1．
    （1）求f（x）的解析式；
    （2）若关于x的方程f（x）=x+m有区间（﹣1，2）上有唯一实数根，求实数的取值范围（注：相等的实数根算一个）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=|2x﹣a|+|2x+1|（a＞0），g（x）=x+2．
    （1）当a=1时，求不等式f（x）≤g（x）的解集；
    （2）若f（x）≥g（x）恒成立，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案