
【题目】已知椭圆![]() 的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于
的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于![]() ,直线l与椭圆C交于
,直线l与椭圆C交于![]() 两点,其中直线l不过原点.
两点,其中直线l不过原点.
(1)求椭圆C的方程;
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,其中
,其中![]() 且
且![]() .记
.记![]() 的面积为S.分别以
的面积为S.分别以![]() 为直径的圆的面积依次为
为直径的圆的面积依次为![]() ,求
,求![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】某农场规划将果树种在正方形的场地内.为了保护果树不被风吹,决定在果树的周围种松树. 在下图里,你可以看到规划种植果树的列数(n),果树数量及松树数量的规律:

(1)按此规律,n = 5时果树数量及松树数量分别为多少;并写出果树数量![]() ,及松树数量
,及松树数量![]() 关于n的表达式
关于n的表达式
(2)定义:![]()
![]() 为
为![]() 增加的速度;现农场想扩大种植面积,问:哪种树增加的速度会更快?并说明理由
增加的速度;现农场想扩大种植面积,问:哪种树增加的速度会更快?并说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网购平台为了解某市居民在该平台的消费情况,从该市使用其平台且每周平均消费额超过100元的人员中随机抽取了100名,并绘制如图所示频率分布直方图,已知中间三组的人数可构成等差数列.
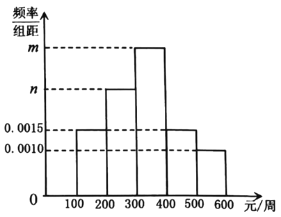
(1)求![]() 的值;
的值;
(2)分析人员对100名调查对象的性别进行统计发现,消费金额不低于300元的男性有20人,低于300元的男性有25人,根据统计数据完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为消费金额与性别有关?
的把握认为消费金额与性别有关?
(3)分析人员对抽取对象每周的消费金额![]() 与年龄
与年龄![]() 进一步分析,发现他们线性相关,得到回归方程
进一步分析,发现他们线性相关,得到回归方程![]() .已知100名使用者的平均年龄为38岁,试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
.已知100名使用者的平均年龄为38岁,试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
![]() 列联表
列联表
男性 | 女性 | 合计 | |
消费金额 | |||
消费金额 | |||
合计 |
临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“二万五千里长征”是1934年10月到1936年10月中国工农红军进行的一次战略转移,是人类历史上的伟大奇迹,向世界展示了中国工农红军的坚强意志,在期间发生了许多可歌可泣的英雄故事.在中国共产党建党![]() 周年之际,某中学组织了“长征英雄事迹我来讲”活动,已知该中学共有高中生
周年之际,某中学组织了“长征英雄事迹我来讲”活动,已知该中学共有高中生![]() 名,用分层抽样的方法从该校高中学生中抽取一个容量为
名,用分层抽样的方法从该校高中学生中抽取一个容量为![]() 的样本参加活动,其中高三年级抽了
的样本参加活动,其中高三年级抽了![]() 人,高二年级抽了
人,高二年级抽了![]() 人,则该校高一年级学生人数为( )
人,则该校高一年级学生人数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,过点
的焦距为2,过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆的右焦点为F,定点![]() ,过点F且斜率不为零的直线l与椭圆交于A,B两点,以线段AP为直径的圆与直线
,过点F且斜率不为零的直线l与椭圆交于A,B两点,以线段AP为直径的圆与直线![]() 的另一个交点为Q,证明:直线BQ恒过一定点,并求出该定点的坐标.
的另一个交点为Q,证明:直线BQ恒过一定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点F(1,0)为抛物线y2=2px(p>0)的焦点,过点F的直线交抛物线于A、B两点,点C在抛物线上,使得△ABC的重心G在x轴上.
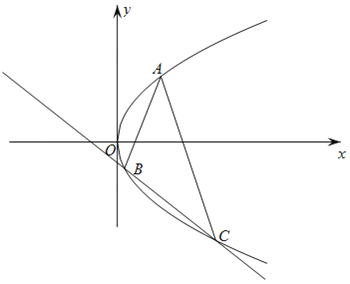
(1)求p的值及抛物线的准线方程 ;
(2)求证:直线OA与直线BC的倾斜角互补;
(3)当xA∈(1,2)时,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校辨论队计划在周六、周日各参加一场辨论赛,分别由正、副队长负责,已知该校辩论队共有10位成员(包含正、副队长),每场比赛除负责人外均另需3位队员(同一队员可同时参加两天的比赛,正、副队长只能参加一场比赛).假设正副队长分别将各自比赛通知的信息独立、随机地发给辩论队8名队员中的3位,且所发信息都能收到.
(1)求辩论队员甲收到队长或副队长所发比赛通知信息的概率;
(2)记辩论队收到正副队长所发比赛通知信息的队员人数为随机变量![]() ,求
,求![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若给定椭圆![]() 和点
和点![]() ,则称直线
,则称直线![]() 为椭圆C的“伴随直线”.
为椭圆C的“伴随直线”.
(1)若![]() 在椭圆C上,判断椭圆C与它的“伴随直线”的位置关系(当直线与椭圆的交点个数为0个、1个、2个时,分别称直线与椭圆相离、相切、相交),并说明理由;
在椭圆C上,判断椭圆C与它的“伴随直线”的位置关系(当直线与椭圆的交点个数为0个、1个、2个时,分别称直线与椭圆相离、相切、相交),并说明理由;
(2)命题:“若点![]() 在椭圆C的外部,则直线
在椭圆C的外部,则直线![]() 与椭圆C必相交.”写出这个命题的逆命题,判断此逆命题的真假,说明理由;
与椭圆C必相交.”写出这个命题的逆命题,判断此逆命题的真假,说明理由;
(3)若![]() 在椭圆C的内部,过N点任意作一条直线,交椭圆C于A、B,交
在椭圆C的内部,过N点任意作一条直线,交椭圆C于A、B,交![]() 于M点(异于A、B),设
于M点(异于A、B),设![]() ,问
,问![]() 是否为定值?说明理由.
是否为定值?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com