
【题目】已知向量 ![]() =(2cosωx,cos2ωx),
=(2cosωx,cos2ωx), ![]() =(sinωx,1)(其中ω>0),令f(x)=
=(sinωx,1)(其中ω>0),令f(x)= ![]() ,且f(x)的最小正周期为π.
,且f(x)的最小正周期为π.
(1)求 ![]() 的值;
的值;
(2)写出 ![]() 上的单调递增区间.
上的单调递增区间.
【答案】
(1)解:f(x)= ![]() =2cosωxsinωx+cos2ωx
=2cosωxsinωx+cos2ωx
=sin2ωx+cos2ωx
= ![]() .
.
∵f(x)的最小正周期为π,∴ω=1.
∴ ![]() .
.
∴ ![]()
(2)解:∵ ![]() ,
,
∴当﹣ ![]() ,
,
即﹣ ![]() (k∈Z)时,f(x)单调递增,
(k∈Z)时,f(x)单调递增,
∵ ![]() ,
,
∴f(x)在 ![]() 上的单调递增区间为
上的单调递增区间为 ![]() .
.
【解析】(1)把向量 ![]() =(2cosωx,cos2ωx),
=(2cosωx,cos2ωx), ![]() =(sinωx,1)代入f(x)=
=(sinωx,1)代入f(x)= ![]() ,利用二倍角公式和两角和的正弦函数化为:
,利用二倍角公式和两角和的正弦函数化为: ![]() ,根据周期求出ω,然后求解
,根据周期求出ω,然后求解 ![]() 的值;(2)利用正弦函数的单调增区间求出函数f(x)的单调增区间,选择适当的k值求出
的值;(2)利用正弦函数的单调增区间求出函数f(x)的单调增区间,选择适当的k值求出 ![]() 上的单调递增区间
上的单调递增区间
【考点精析】利用正弦函数的单调性对题目进行判断即可得到答案,需要熟知正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数.
上是减函数.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间![]() (单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为
(单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,绘制出频率分布直方图.
,绘制出频率分布直方图.
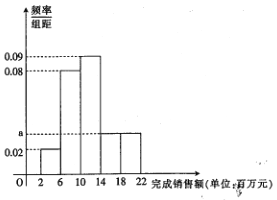
(1)求![]() 的值,并计算完成年度任务的人数;
的值,并计算完成年度任务的人数;
(2)用分层抽样从这200位销售员中抽取容量为25的样本,求这5组分别应抽取的人数;
(3)现从(2)中完成年度任务的销售员中随机选取2位,奖励海南三亚三日游,求获得此奖励的2位销售员在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(cosx,﹣
=(cosx,﹣ ![]() ),
), ![]() =(sinx+cosx,1),f(x)=
=(sinx+cosx,1),f(x)= ![]()
![]() ,
,
(1)若0<α< ![]() ,sinα=
,sinα= ![]() ,求f(α)的值;
,求f(α)的值;
(2)求函数f(x)的最小正周期及单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π),在同一周期内,当x= ![]() 时,f(x)取得最大值3;当x=
时,f(x)取得最大值3;当x= ![]() 时,f(x)取得最小值﹣3.
时,f(x)取得最小值﹣3.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“随机模拟方法”计算曲线![]() 与直线
与直线![]() ,
, ![]() 所围成的曲边三角形的面积时,用计算机分别产生了10个在区间
所围成的曲边三角形的面积时,用计算机分别产生了10个在区间![]() 上的均匀随机数
上的均匀随机数![]() 和10个区间
和10个区间![]() 上的均匀随机数
上的均匀随机数![]() (
(![]() ,
, ![]() ),其数据如下表的前两行.
),其数据如下表的前两行.
| 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
| 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
| 0.90 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
由此可得这个曲边三角形面积的一个近似值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com