
【题目】数列{2n﹣1}的前n项1,3,7,…,2n﹣1组成集合![]() (n∈N*),从集合An中任取k(k=1,2,3,…,n)个数,其所有可能的k个数的乘积的和为Tk(若只取一个数,规定乘积为此数本身),记Sn=T1+T2+…+Tn,例如当n=1时,A1={1},T1=1,S1=1;当n=2时,A2={1,3},T1=1+3,T2=1×3,S2=1+3+1×3=7,试写出Sn=__.
(n∈N*),从集合An中任取k(k=1,2,3,…,n)个数,其所有可能的k个数的乘积的和为Tk(若只取一个数,规定乘积为此数本身),记Sn=T1+T2+…+Tn,例如当n=1时,A1={1},T1=1,S1=1;当n=2时,A2={1,3},T1=1+3,T2=1×3,S2=1+3+1×3=7,试写出Sn=__.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】对于定义域为R的函数![]() ,若函数
,若函数![]() 是奇函数,则称
是奇函数,则称![]() 为正弦奇函数.已知
为正弦奇函数.已知![]() 是单调递增的正弦奇函数,其值域为R,
是单调递增的正弦奇函数,其值域为R,![]() .
.
(1)已知![]() 是正弦奇函数,证明:“
是正弦奇函数,证明:“![]() 为方程
为方程![]() 的解”的充要条件是“
的解”的充要条件是“![]() 为方程
为方程![]() 的解”;
的解”;
(2)若![]()
![]() ,求
,求![]() 的值;
的值;
(3)证明:![]() 是奇函数.
是奇函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在圆![]() 上任取一点
上任取一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线段
轴的垂线段![]() ,
,![]() 为垂足,当点
为垂足,当点![]() 在圆上运动时,点
在圆上运动时,点![]() 在线段
在线段![]() 上,且
上,且![]() ,点
,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过抛物线![]() :
:![]() 的焦点
的焦点![]() 作直线
作直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,过
两点,过![]() 且与直线
且与直线![]() 垂直的直线交曲线
垂直的直线交曲线![]() 于另一点
于另一点![]() ,求
,求![]() 面积的最小值,以及取得最小值时直线
面积的最小值,以及取得最小值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年11月河南省三门峡市成功入围“十佳魅力中国城市”,吸引了大批投资商的目光,一些投资商积极准备投入到“魅力城市”的建设之中.某投资公司准备在2018年年初将四百万元投资到三门峡下列两个项目中的一个之中.
项目一:天坑院是黄土高原地域独具特色的民居形式,是人类“穴居”发展史演变的实物见证.现准备投资建设20个天坑院,每个天坑院投资0.2百万元,假设每个天坑院是否盈利是相互独立的,据市场调研,到2020年底每个天坑院盈利的概率为![]()
![]() ,若盈利则盈利投资额的40%,否则盈利额为0.
,若盈利则盈利投资额的40%,否则盈利额为0.
项目二:天鹅湖国家湿地公园是一处融生态、文化和人文地理于一体的自然山水景区.据市场调研,投资到该项目上,到2020年底可能盈利投资额的50%,也可能亏损投资额的30%,且这两种情况发生的概率分别为p和![]() .
.
(1)若投资项目一,记![]() 为盈利的天坑院的个数,求
为盈利的天坑院的个数,求![]() (用p表示);
(用p表示);
(2)若投资项目二,记投资项目二的盈利为![]() 百万元,求
百万元,求![]() (用p表示);
(用p表示);
(3)在(1)(2)两个条件下,针对以上两个投资项目,请你为投资公司选择一个项目,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 定义在实数集
定义在实数集![]() 上的函数,把方程
上的函数,把方程![]() 称为函数
称为函数![]() 的特征方程,特征方程的两个实根
的特征方程,特征方程的两个实根![]() ,
,![]()
![]() 称为
称为![]() 的特征根.
的特征根.
(1)讨论函数的奇偶性,并说明理由;
(2)求![]() 表达式;
表达式;
(3)把函数![]() ,
,![]() 的最大值记作
的最大值记作![]() 、最小值记作
、最小值记作![]() ,令
,令![]() ,若
,若![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 上各点的纵坐标伸长为原来的
上各点的纵坐标伸长为原来的![]() 倍(横坐标不变)得到曲线
倍(横坐标不变)得到曲线![]() ,求
,求![]() 的参数方程;
的参数方程;
(2)若![]() ,
,![]() 分别是直线
分别是直线![]() 与曲线
与曲线![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,当
,当![]() ,
,![]() 时,
时,![]() 的值域为
的值域为![]() ,
,![]() ,当
,当![]() ,
,![]() 时,
时,![]() 的值域为
的值域为![]() ,
,![]() ,依此类推,一般地,当
,依此类推,一般地,当![]() ,
,![]() 时,
时,![]() 的值域为
的值域为![]() ,
,![]() ,其中
,其中![]() 、
、![]() 为常数,且
为常数,且![]() ,
,![]() .
.
(1)若![]() ,求数列
,求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)若![]() ,问是否存在常数
,问是否存在常数![]() ,使得数列
,使得数列![]() 满足
满足![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)若![]() ,设数列
,设数列![]() ,
,![]() 的前
的前![]() 项和分别为
项和分别为![]() ,
,![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图数表:

每一行都是首项为1的等差数列,第![]() 行的公差为
行的公差为![]() ,且每一列也是等差数列,设第
,且每一列也是等差数列,设第![]() 行的第
行的第![]() 项为
项为![]() .
.
(1)证明:![]() 成等差数列,并用
成等差数列,并用![]() 表示
表示![]() (
(![]() );
);
(2)当![]() 时,将数列
时,将数列![]() 分组如下:(
分组如下:(![]() ),(
),(![]() ),(
),(![]() ),…(每组数的个数构成等差数列). 设前
),…(每组数的个数构成等差数列). 设前![]() 组中所有数之和为
组中所有数之和为![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)在(2)的条件下,设![]() 是不超过20的正整数,当
是不超过20的正整数,当![]() 时,求使得不等式
时,求使得不等式![]() 恒成立的所有
恒成立的所有![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
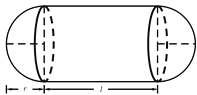
【题目】某加油站拟建造如图所示的铁皮储油罐(不计厚度,长度单位为米),其中储油罐的中间为圆柱形,左右两端均为半球形,![]() (
(![]() 为圆柱的高,为球的半径,
为圆柱的高,为球的半径,![]() ).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为![]() 千元,半球形部分每平方米建造费用为
千元,半球形部分每平方米建造费用为![]() 千元.设该储油罐的建造费用为
千元.设该储油罐的建造费用为![]() 千元.
千元.
(1) 写出![]() 关于
关于![]() 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(2) 若预算为![]() 万元,求所能建造的储油罐中
万元,求所能建造的储油罐中![]() 的最大值(精确到
的最大值(精确到![]() ),并求此时储油罐的体积
),并求此时储油罐的体积![]() (单位: 立方米,精确到
(单位: 立方米,精确到![]() 立方米).
立方米).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com