
【题目】如图,AB是⊙O的一条切线,切点为B,直线ADE、CFD、CGE都是⊙O的割线,已知AC=AB. 
(1)若CG=1,CD=4.求 ![]() 的值.
的值.
(2)求证:FG∥AC.
【答案】
(1)解:∵四边形DEGF内接于⊙O,
∴∠CGF=∠CDE,∠CFG=∠CED.
因此△CGF∽△CDE,可得 ![]() =
= ![]() ,
,
又∵CG=1,CD=4,
∴ ![]() =4
=4
(2)解:证明:∵AB与⊙O的相切于点B,ADE是⊙O的割线,
∴AB2=ADAE,
∵AB=AC,
∴AC2=ADAE,可得 ![]() =
= ![]() ,
,
又∵∠EAC=∠DAC,
∴△ADC∽△ACE,可得∠ADC=∠ACE,
∵四边形DEGF内接于⊙O,
∴∠ADC=∠EGF,
因此∠EGF=∠ACE,可得GF∥AC
【解析】(1)根据圆内接四边形的性质,证出∠CGF=∠CDE且∠CFG=∠CED,可得△CGF∽△CDE,因此 ![]() =
= ![]() =4;(2)根据切割线定理证出AB2=ADAE,所以AC2=ADAE,证出
=4;(2)根据切割线定理证出AB2=ADAE,所以AC2=ADAE,证出 ![]() =
= ![]() ,结合∠EAC=∠DAC得到△ADC∽△ACE,所以∠ADC=∠ACE.再根据圆内接四边形的性质得∠ADC=∠EGF,从而∠EGF=∠ACE,可得GF∥AC.
,结合∠EAC=∠DAC得到△ADC∽△ACE,所以∠ADC=∠ACE.再根据圆内接四边形的性质得∠ADC=∠EGF,从而∠EGF=∠ACE,可得GF∥AC.


科目:高中数学 来源: 题型:
【题目】如图1,平行四边形ABCD中,AB=2AD,∠DAB=60°,M是BC的中点.将△ADM沿DM折起,使面ADM⊥面MBCD,N是CD的中点,图2所示. 
(Ⅰ)求证:CM⊥平面ADM;
(Ⅱ)若P是棱AB上的动点,当 ![]() 为何值时,二面角P﹣MC﹣B的大小为60°.
为何值时,二面角P﹣MC﹣B的大小为60°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于实数x,符号[x]表示不超过x的最大整数,例如[π]=3,[﹣1.08]=﹣2,定义函数f(x)=x﹣[x],则下列命题中正确的是
①函数f(x)的最大值为1; ②函数f(x)的最小值为0;
③方程![]() 有无数个根; ④函数f(x)是增函数.
有无数个根; ④函数f(x)是增函数.
A. ②③ B. ①②③ C. ② D. ③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为(-3,3),
满足f(-x)=-f(x),且对任意x,y,都有f(x)-f(y)=f(x-y),当x<0时,f(x)>0,f(1)=-2.
(1)求f(2)的值;
(2)判断f(x)的单调性,并证明;
(3)若函数g(x)=f(x-1)+f(3-2x),求不等式g(x)≤0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,且anan+1=2n , n∈N* , 则数列{an}的通项公式为( )
A.an=( ![]() )n﹣1
)n﹣1
B.an=( ![]() )n
)n
C.an= ![]()
D.an= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE= ![]() BB1 , C1F=
BB1 , C1F= ![]() CC1 .
CC1 . 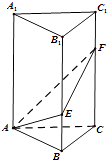
(1)求平面AEF与平面ABC所成角α的余弦值;
(2)若G为BC的中点,A1G与平面AEF交于H,且设 ![]() =
= ![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公差不为0的等差数列![]() 中,已知
中,已知![]() 且
且![]() ,其前
,其前![]() 项和
项和![]() 的最大值为( )
的最大值为( )
A. 25 B. 26 C. 27 D. 28
【答案】B
【解析】设等差数列![]() 的公差为
的公差为![]() ,
,
∵![]() ,
,
∴![]() ,
,
整理得![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
∴当![]() 时,
时, ![]() .
.
故![]() 最大,且
最大,且![]() .选B.
.选B.
点睛:求等差数列前n项和最值的常用方法:
①利用等差数列的单调性, 求出其正负转折项,便可求得和的最值;
②将等差数列的前n项和![]() (A、B为常数)看作关于n的二次函数,根据二次函数的性质求最值.
(A、B为常数)看作关于n的二次函数,根据二次函数的性质求最值.
【题型】单选题
【结束】
9
【题目】如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )
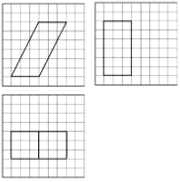
A. ![]() B.
B. ![]() C. 90 D. 81
C. 90 D. 81
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com