解:∵sinxcosx=

sin2x,cos
2x=

(1+cos2x)
∴f(x)=2cosx(sinx+cosx)=2sinxcosx+2cos
2x=sin2x+cos2x+1.
由此可得f(x)=

sin(2x+

)+1
(1)∵x∈[
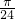
,
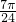
],∴2x+

∈[

,

]
由此可得,当2x+

=

,即x=

时函数的最大值为1+

当2x+

=

,即x=
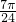
时函数的最小值为1+

=

.
∴当x∈[
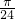
,
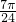
],函数f(x)的值域为[1+

,1+

]
(2)由f(

)=

sin(θ+

)+1=

,得sin(θ+

)=

∵θ∈(0,π),得θ+

∈(

,

)
∴结合sin(θ+

)=


且为正数,得θ+

∈(

,π)
因此cos(θ+

)=
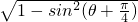
=

∴cosθ=cos[(θ+

)-

]=

×

+

×

=

可得cos2θ=2cos
2θ-1=2×

-1=

.
分析:(1)利用二倍角三角函数公式,结合辅助角公式化简整理得f(x)=

sin(2x+

)+1,再讨论得出2x+

∈[

,

],结合三角函数的图象与性质即可得到函数f(x)的值域;
(2)代入(1)中的表达式,由f(

)=

得sin(θ+

)=

,结合θ∈(0,π)算出cos(θ+

)=

,再利用配角得到cosθ=cos[(θ+

)-

]=

,最后利用二倍角余弦公式即可得到cos2θ的值.
点评:本题给出三角函数表达式,求函数值域并求三角函数值,着重考查了三角恒等变形、三角函数的图象与性质等知识点,属于中档题.

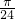 ,
,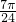 ],求函数f(x)的值域;
],求函数f(x)的值域; )=
)= ,θ∈(0,π),求cos2θ的值.
,θ∈(0,π),求cos2θ的值. sin2x,cos2x=
sin2x,cos2x= (1+cos2x)
(1+cos2x) sin(2x+
sin(2x+ )+1
)+1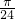 ,
,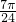 ],∴2x+
],∴2x+ ∈[
∈[ ,
, ]
] =
= ,即x=
,即x= 时函数的最大值为1+
时函数的最大值为1+
 =
= ,即x=
,即x=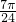 时函数的最小值为1+
时函数的最小值为1+ =
= .
.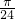 ,
,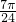 ],函数f(x)的值域为[1+
],函数f(x)的值域为[1+ ,1+
,1+ ]
] )=
)= sin(θ+
sin(θ+ )+1=
)+1= ,得sin(θ+
,得sin(θ+ )=
)=
 ∈(
∈( ,
, )
) )=
)=
 且为正数,得θ+
且为正数,得θ+ ∈(
∈( ,π)
,π) )=
)=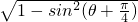 =
=
 )-
)- ]=
]= ×
× +
+ ×
× =
=
 -1=
-1= .
. sin(2x+
sin(2x+ )+1,再讨论得出2x+
)+1,再讨论得出2x+ ∈[
∈[ ,
, ],结合三角函数的图象与性质即可得到函数f(x)的值域;
],结合三角函数的图象与性质即可得到函数f(x)的值域; )=
)= 得sin(θ+
得sin(θ+ )=
)= ,结合θ∈(0,π)算出cos(θ+
,结合θ∈(0,π)算出cos(θ+ )=
)= ,再利用配角得到cosθ=cos[(θ+
,再利用配角得到cosθ=cos[(θ+ )-
)- ]=
]= ,最后利用二倍角余弦公式即可得到cos2θ的值.
,最后利用二倍角余弦公式即可得到cos2θ的值.

 全优点练单元计划系列答案
全优点练单元计划系列答案