
【题目】某生物研究所为研发一种新疫苗,在200只小白鼠身上进行科研对比实验,得到如下统计数据:
未感染病毒 | 感染病毒 | 总计 | |
未注射疫苗 | 30 |
|
|
注射疫苗 | 70 |
|
|
总计 | 100 | 100 | 200 |
现从未注射疫苗的小白鼠中任取1只,取到“感染病毒”的小白鼠的概率为![]() .
.
(Ⅰ)能否有![]() 的把握认为注射此种疫苗有效?
的把握认为注射此种疫苗有效?
(Ⅱ)在未注射疫苗且未感染病毒与注射疫苗且感染病毒的小白鼠中,分别抽取3只进行病例分析,然后从这6只小白鼠中随机抽取2只对注射疫苗情况进行核实,求抽到的2只均是注射疫苗且感染病毒的小白鼠的概率.
附: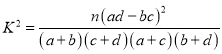 ,
,![]() ,
,
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(Ⅰ)有![]() 的把握认为注射此种疫苗有效;(Ⅱ)
的把握认为注射此种疫苗有效;(Ⅱ)![]()
【解析】
(Ⅰ)根据题意,从未注射疫苗的小白鼠中任取1只,取到“感染病毒”的小白鼠的概率为![]() .可求
.可求![]() ,根据
,根据![]() 列联表可求得其他数据,运用独立性检验公式,计算即可求解;
列联表可求得其他数据,运用独立性检验公式,计算即可求解;
(Ⅱ)根据题意,将抽取出来的小白鼠分别标记,列出所有基本事件,根据古典概型计算概率.
(Ⅰ)由条件知![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
所以有![]() 的把握认为注射此种疫苗有效.
的把握认为注射此种疫苗有效.
(Ⅱ)由条件知将抽到的3只未注射疫苗且未感染病毒的小白鼠记为![]() ,
,![]() ,
,![]() ,将抽到的3只注射疫苗且感染病毒的小白鼠分别记为
,将抽到的3只注射疫苗且感染病毒的小白鼠分别记为![]() ,
,![]() ,
,![]() ,从这6只小白鼠中随机抽取2只共有
,从这6只小白鼠中随机抽取2只共有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 等15种可能,
等15种可能,
抽到的2只均是注射疫苗且感染病毒的小白鼠有![]() ,
,![]() ,
,![]() 等3种情况,
等3种情况,
所以抽到的2只均是注射疫苗且感染病毒的小白鼠的概率为![]() .
.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】某高速公路全程设有2n(n≥4,![]() )个服务区.为加强驾驶人员的安全意识,现规划在每个服务区的入口处设置醒目的宣传标语A或宣传标语B.
)个服务区.为加强驾驶人员的安全意识,现规划在每个服务区的入口处设置醒目的宣传标语A或宣传标语B.
(1)若每个服务区入口处设置宣传标语A的概率为![]() ,入口处设置宣传标语B的服务区有X个,求X的数学期望;
,入口处设置宣传标语B的服务区有X个,求X的数学期望;
(2)试探究全程两种宣传标语的设置比例,使得长途司机在走该高速全程中,随机选取3个服务区休息,看到相同宣传标语的概率最小,并求出其最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,P是椭圆的上顶点,过点P作斜率为
,P是椭圆的上顶点,过点P作斜率为![]() 的直线l交椭圆于另一点A,设点A关于原点的对称点为B
的直线l交椭圆于另一点A,设点A关于原点的对称点为B
(1)求![]() 面积的最大值;
面积的最大值;
(2)设线段PB的中垂线与y轴交于点N,若点N在椭圆内部,求斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知函数![]() 的图象与y轴交于点
的图象与y轴交于点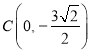 ,与x轴交于A,B两点,其中
,与x轴交于A,B两点,其中![]() ,
,![]() .
.

(1)求函数![]() 的解析式;
的解析式;
(2)将函数![]() 图象上所有点的横坐标缩短为原来的
图象上所有点的横坐标缩短为原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象,求函数
的图象,求函数![]() 的单调递减区间.
的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把一块边长为![]() 的正六边形铁皮,沿图中的虚线(虛线与正六边形的对应边垂直)剪去六个全等的四边形(阴影部分),折起六个矩形焊接制成一个正六棱柱形的无盖容器(焊接损耗忽略),设容器的底面边长为
的正六边形铁皮,沿图中的虚线(虛线与正六边形的对应边垂直)剪去六个全等的四边形(阴影部分),折起六个矩形焊接制成一个正六棱柱形的无盖容器(焊接损耗忽略),设容器的底面边长为![]() .
.

(1)若![]() ,且该容器的表面积为
,且该容器的表面积为![]() 时,在该容器内注入水,水深为
时,在该容器内注入水,水深为![]() ,若将一根长度为
,若将一根长度为![]() 的玻璃棒(粗细忽略)放入容器内,一端置于
的玻璃棒(粗细忽略)放入容器内,一端置于![]() 处,另一端置于侧棱
处,另一端置于侧棱![]() 上,忽略铁皮厚度,求玻璃棒浸人水中部分的长度;
上,忽略铁皮厚度,求玻璃棒浸人水中部分的长度;
(2)求该容器的底面边长![]() 的范围,使得该容器的体积始终不大于
的范围,使得该容器的体积始终不大于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知等边![]() 的边长为3,点
的边长为3,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() .如图2,将
.如图2,将![]() 沿
沿![]() 折起到
折起到![]() 的位置.
的位置.
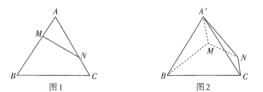
(1)求证:平面![]() 平面
平面![]() ;
;
(2)给出三个条件:①![]() ;②二面角
;②二面角![]() 大小为
大小为![]() ;③
;③![]() .在这三个条件中任选一个,补充在下面问题的条件中,并作答:在线段
.在这三个条件中任选一个,补充在下面问题的条件中,并作答:在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的长;若不存在,请说明理由.注:如果多个条件分别解答,按第一个解答给分
的长;若不存在,请说明理由.注:如果多个条件分别解答,按第一个解答给分
查看答案和解析>>
科目:高中数学 来源: 题型:
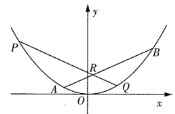
【题目】如图,斜率为![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,已知点
两点,已知点![]() 的横坐标比点
的横坐标比点![]() 的横坐标大4,直线
的横坐标大4,直线![]() 交线段
交线段![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() .
.
(1)若点![]() 的横坐标等于0,求
的横坐标等于0,求![]() 的值;
的值;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com