
分析 (1)由正弦定理化简已知等式可得$\frac{cosA}{cosB}=-\frac{sinA}{sinB+2sinC}$,解得cosA=-$\frac{1}{2}$,根据A的范围即可解得A的值.
(2)由(1)及三角函数恒等变换的应用可得sinBsinC=$\frac{1}{2}$sin(2B+$\frac{π}{6}$)-$\frac{1}{4}$,由范围0$<B<\frac{π}{3}$,可得$\frac{π}{6}<$2B+$\frac{π}{6}$$<\frac{5π}{6}$,利用正弦函数的图象和性质即可解得sinBsinC的最大值.
解答 解:(1)由$\frac{cosA}{cosB}=-\frac{a}{b+2c}$.得$\frac{cosA}{cosB}=-\frac{sinA}{sinB+2sinC}$,
∴2cosAsinC=-sin(A+B)=-sinC
∴cosA=-$\frac{1}{2}$,
∴由A为三角形内角,可得:A=$\frac{2π}{3}$.
(2)∵sinBsinC=sinBsin($\frac{π}{3}-B$)=$\frac{1}{2}$sin(2B+$\frac{π}{6}$)-$\frac{1}{4}$,
∵0$<B<\frac{π}{3}$,$\frac{π}{6}<$2B+$\frac{π}{6}$$<\frac{5π}{6}$,
∴当sin(2B+$\frac{π}{6}$)=1即B=$\frac{π}{6}$时,sinBsinC取得最大值$\frac{1}{4}$.
点评 本题主要考查了正弦定理,正弦函数的图象和性质以及三角函数恒等变换的应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
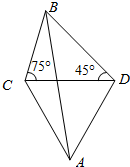 如图,某炮兵阵地位于A点,两观察所分别位于C,D两点.已知△ACD为正三角形,且DC=$\sqrt{3}$ km,当目标出现在B点时,测得∠BCD=75°,∠CDB=45°,求炮兵阵地与目标的距离.
如图,某炮兵阵地位于A点,两观察所分别位于C,D两点.已知△ACD为正三角形,且DC=$\sqrt{3}$ km,当目标出现在B点时,测得∠BCD=75°,∠CDB=45°,求炮兵阵地与目标的距离.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{2}{3},1$] | B. | ($\frac{2}{3},1$] | C. | [$\frac{2}{3},1$) | D. | ($\frac{2}{3},1$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com