
【题目】(本题![]() 分)
分)
已知函数![]() ,若存在
,若存在![]() ,使得
,使得![]() ,则称
,则称![]() 是函数
是函数![]() 的一个不动点,设二次函数
的一个不动点,设二次函数![]() .
.
(Ⅰ)当![]() ,
, ![]() 时,求函数
时,求函数![]() 的不动点.
的不动点.
(Ⅱ)若对于任意实数![]() ,函数
,函数![]() 恒有两个不同的不动点,求实数
恒有两个不同的不动点,求实数![]() 的取值范围.
的取值范围.
(Ⅲ)在(![]() )的条件下,若函数
)的条件下,若函数![]() 的图象上
的图象上![]() ,
, ![]() 两点的横坐标是函数
两点的横坐标是函数![]() 的不动点,且直线
的不动点,且直线![]() 是线段
是线段![]() 的垂直平分线,求实数
的垂直平分线,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)实数
(3)实数![]() 的取值范围是
的取值范围是![]() .
.
【解析】试题分析:Ⅰ)把![]() ,
, ![]() 代入方程f(x)=x,解出x即可;
代入方程f(x)=x,解出x即可;
(Ⅱ)方程f(x)=x恒有两个不相等的实数根,即方程ax2+(b+1)x+b﹣2=x恒有两个不相等的实数根,则 ![]() 对任意b恒成立,根据二次函数的性质可得a的不等式;
对任意b恒成立,根据二次函数的性质可得a的不等式;
(Ⅲ)设函数f(x)的两个不同的不动点为x1,x2,则A(x1,x1),B(x2,x2),且x1,x2是ax2+bx+b﹣2=0的两个不等实根,则![]() ,由题意可得k=﹣1,且AB中点
,由题意可得k=﹣1,且AB中点![]() 在直线
在直线![]() 上,代入可得a,b的关系式,分离出b后根据a的范围可得b的范围;
上,代入可得a,b的关系式,分离出b后根据a的范围可得b的范围;
试题解析:
(Ⅰ)当![]() ,
, ![]() 时,
时, ![]() ,
,
由![]() 得
得![]() ,解得
,解得![]() 或
或![]() .
.
∴函数![]() 的不动点为
的不动点为![]() ,
, ![]() .
.
(Ⅱ)∵对于任意实数![]() ,函数
,函数![]() 恒有两个不同的不动点,
恒有两个不同的不动点,
∴对于任意实数![]() ,方程
,方程![]() 恒有两个不相等的实数根,
恒有两个不相等的实数根,
即方程![]() 恒有两个不相等的实数根,
恒有两个不相等的实数根,
∴![]() ,即对任意实数
,即对任意实数![]() ,
, ![]() 恒成立,
恒成立,
∴![]() ,
,
解得![]() .
.
(Ⅲ)设函数![]() 的两个不同的不动点为
的两个不同的不动点为![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,且
,且![]() ,
, ![]() 是
是![]() 的两个不等实根,
的两个不等实根,
所以![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,线段
,线段![]() 中点坐标为
中点坐标为![]() ,
,
∵直线![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,
∴![]() ,且
,且![]() 在直线
在直线![]() 上,
上,
即![]() ,
, ![]() ,
,
∴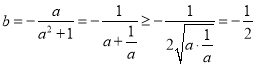 ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
又∵![]() ,
,
∴实数![]() 的取值范围是
的取值范围是![]() .
.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】若函数![]() 对定义域D内的每一个x1,都存在唯一的x2∈D,使得
对定义域D内的每一个x1,都存在唯一的x2∈D,使得![]() 成立,则称f (x)为“自倒函数”.给出下列命题:
成立,则称f (x)为“自倒函数”.给出下列命题:
①![]() 是自倒函数;
是自倒函数;
②自倒函数f (x)可以是奇函数;
③自倒函数f (x)的值域可以是R;
④若![]() 都是自倒函数,且定义域相同,则
都是自倒函数,且定义域相同,则![]() 也是自倒函数.
也是自倒函数.
则以上命题正确的是_______(写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
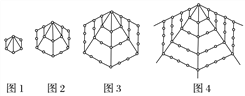
【题目】在一次珠宝展览会上,某商家展出一套珠宝首饰,第1件首饰是1颗珠宝,第2件首饰是由6颗珠宝构成的如图1所示的正六边形,第3件首饰是由15颗珠宝构成的如图2所示的正六边形,第4件首饰是由28颗珠宝构成的如图3所示的正六边形,第5件首饰是由45颗珠宝构成的如图4所示的正六边形,以后每件首饰都在前一件的基础上,按照这种规律增加一定数量的珠宝,使它构成更大的正六边形,依此推断:
(1)第6件首饰上应有________颗珠宝;
(2)前n(n∈N*)件首饰所用珠宝总颗数为________.(结果用n表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·成都高中毕业第一次诊断)已知双曲线![]() (a>0,b>0)的左、右焦点分别为F1,F2,双曲线上一点P满足PF2⊥x轴.若|F1F2|=12,|PF2|=5,则该双曲线的离心率为( )
(a>0,b>0)的左、右焦点分别为F1,F2,双曲线上一点P满足PF2⊥x轴.若|F1F2|=12,|PF2|=5,则该双曲线的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4吨,硝酸盐18吨;生产1车皮乙种肥料需要的主要原料是磷酸盐1吨,硝酸盐15吨.现库存磷酸盐10吨,硝酸盐66吨,在此基础上生产这两种混合肥料.如果生产1车皮甲种肥料产生的利润为12 000元,生产1车皮乙种肥料产生的利润为7 000元,那么可产生的最大利润是( )
A. 29 000元 B. 31 000元 C. 38 000元 D. 45 000元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出集合![]() .
.
(1)若![]() ,求证:函数
,求证:函数![]() ;
;
(2)由(1)分析可知, ![]() 是周期函数且是奇函数,于是张三同学得出两个命
是周期函数且是奇函数,于是张三同学得出两个命
题:命题甲:集合![]() 中的元素都是周期函数.命题乙:集合
中的元素都是周期函数.命题乙:集合![]() 中的元素都是奇函数. 请对此
中的元素都是奇函数. 请对此
给出判断,如果正确,请证明;如果不正确,请举反例;
(3)若![]() ,数列
,数列![]() 满足:
满足: ![]() ,且
,且![]()
![]() ,数列
,数列![]() 的前
的前![]() 项
项
和为![]() ,试问是否存在实数
,试问是否存在实数![]() 、
、![]() ,使得任意的
,使得任意的![]() ,都有
,都有![]() 成立,若
成立,若
存在,求出![]() 、
、![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x和直线l:x=-1.
(1)若曲线C上存在一点Q,它到l的距离与到坐标原点O的距离相等,求Q点的坐标;
(2)过直线l上任一点P作抛物线的两条切线,切点记为A,B,求证:直线AB过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com