
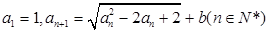
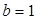 ,求
,求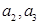 及数列
及数列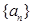 的通项公式;
的通项公式;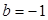 ,问:是否存在实数
,问:是否存在实数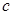 使得
使得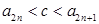 对所有
对所有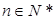 成立?证明你的结论.
成立?证明你的结论.
 ;(2)存在,
;(2)存在,


 是等差数列,可先求数列
是等差数列,可先求数列 再求数列
再求数列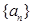 的通项公式;也可以先根据数列
的通项公式;也可以先根据数列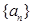 的前几项归纳出数列
的前几项归纳出数列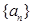 的通项公式,然后由数学归纳法证明.
的通项公式,然后由数学归纳法证明. 构造函数
构造函数 ,
, ,然后结合函数
,然后结合函数 的单调性,用数学归纳法证明
的单调性,用数学归纳法证明 即可.
即可.

 是首项为0公差为1的等差数列,
是首项为0公差为1的等差数列, =
= ,即
,即

 .因此猜想
.因此猜想 .
. 时结论显然成立.
时结论显然成立. 时结论成立,即
时结论成立,即 .则
.则
 时结论成立.
时结论成立.
 ,则
,则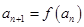 .
. ,即
,即 ,解得
,解得 .
.
 时,
时, ,所以
,所以 ,结论成立.
,结论成立. 时结论成立,即
时结论成立,即
 在
在 上为减函数,从而
上为减函数,从而

 在
在 上为减函数得
上为减函数得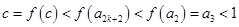 .
. ,因此
,因此 ,这就是说,当
,这就是说,当 时结论成立.
时结论成立. 存在,其中一个值为
存在,其中一个值为 .
. ,则
,则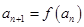
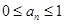
 ①
① 时,结论明显成立.
时,结论明显成立. 时结论成立,即
时结论成立,即
 在
在 上为减函数,从而
上为减函数,从而
 这就是说,当
这就是说,当 时结论成立,故①成立.
时结论成立,故①成立.
 ②
② 时,
时, ,有
,有 ,即当
,即当 时结论②成立
时结论②成立 时,结论成立,即
时,结论成立,即
 在
在 上为减函数,得
上为减函数,得

 时②成立,所以②对一切
时②成立,所以②对一切 成立.
成立.


 在
在 上为减函数得
上为减函数得

 解得
解得 .
. 使
使 对一切
对一切 成立.
成立.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源:不详 题型:解答题
 满足:
满足: ,且
,且 、
、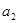 、
、 成等比数列.
成等比数列. 的通项公式.
的通项公式. 为数列
为数列 的前
的前 项和,是否存在正整数
项和,是否存在正整数 ,使得
,使得 若存在,求
若存在,求 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
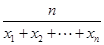 为n个正数x1,x2,…,xn的“平均倒数”,若正项数列{cn}的前n项的“平均倒数”为
为n个正数x1,x2,…,xn的“平均倒数”,若正项数列{cn}的前n项的“平均倒数”为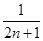 ,则数列{cn}的通项公式为cn=________.
,则数列{cn}的通项公式为cn=________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,如果
,如果 为完全平方数,则称数列
为完全平方数,则称数列 具有“P性质”,如果数列
具有“P性质”,如果数列 不具有“P性质”,只要存在与
不具有“P性质”,只要存在与 不是同一数列的
不是同一数列的 ,且
,且 同时满足下面两个条件:①
同时满足下面两个条件:① 是
是 的一个排列;②数列
的一个排列;②数列 具有“P性质”,则称数列
具有“P性质”,则称数列 具有“变换P性质”,下面三个数列:
具有“变换P性质”,下面三个数列: 的前n项和为
的前n项和为 .
.| A.③ | B.①③ | C.①② | D.①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com