
【题目】已知数列{an}的前n项和为Sn , 且Sn=2an﹣2,数列{bn}满足b1=1,且bn+1=bn+2.
(1)求数列{an},{bn}的通项公式;
(2)设cn= ![]() ,求数列{cn}的前2n项和T2n .
,求数列{cn}的前2n项和T2n .
【答案】
(1)解:当n=1,a1=2;
当n≥2时,an=Sn﹣Sn﹣1=2an﹣2an﹣1,
∴an=2an﹣1.
∴{an}是等比数列,公比为2,首项a1=2,
∴ ![]() .
.
由bn+1=bn+2,得{bn}是等差数列,公差为2.
又首项b1=1,
∴bn=2n﹣1
(2)解: ![]()
∴ ![]() +[3+7+…+(4n﹣1)]
+[3+7+…+(4n﹣1)]
= ![]()
= ![]()
【解析】(1)当n=1,可求a1 , n≥2时,an=Sn﹣Sn﹣1可得an与an﹣1的递推关系,结合等比数列的通项公式可求an , 由bn+1=bn+2,可得{bn}是等差数列,结合等差数列的通项公式可求bn . (2)由题意可得 ![]() ,然后结合等差数列与等比数列的求和公式,利用分组求和即可求解
,然后结合等差数列与等比数列的求和公式,利用分组求和即可求解
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系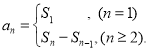 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】已知集合A是函数y=lg(6+5x﹣x2)的定义域,集合B是不等式x2﹣2x+1﹣a2≥0(a>0)的解集.p:x∈A,q:x∈B.
(1)若A∩B=,求a的取值范围;
(2)若¬p是q的充分不必要条件,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+bx2+cx在x=±1处取得极值,且在x=0处的切线的斜率为﹣3.
(1)求f(x)的解析式;
(2)求过点A(2,2)的切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上(如图).该股票在30天内(包括第30天)的日交易量Q(万股)与时间t(天)的函数关系式为Q=40﹣t(0≤t≤30且t∈N). 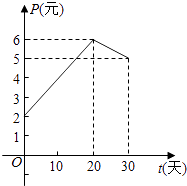
(1)根据提供的图象,求出该种股票每股的交易价格P(元)与时间t(天)所满足的函数关系式;
(2)用y(万元)表示该股票日交易额(日交易额=日交易量×每股的交易价格),写出y关于t的函数关系式,并求出这30天中第几天日交易额最大,最大值为多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com