
分析 根据数列的递推公式可得数列{an}是以1为首项,以1为公差的等差数列,an=n,则bn=(-1)n$\frac{2n+1}{{a}_{n}•{a}_{n+1}}$=(-1)n•($\frac{1}{n}$+$\frac{1}{n+1}$),再分n为偶数和奇数两种情况求出前n项和.
解答 解:∵2Sn=an•an+1(n∈N*).
当n≥2时,2Sn-1=an-1•an,
∴2an=2Sn-2Sn-1=an(an+1-an-1),
∵a1=1,
∴an≠0
∴an+1-an-1=2,
∴(an+1-an)+(an-an-1)=2,
∴an-an-1=1,
∴数列{an}是以1为首项,以1为公差的等差数列,
∴an=1+(n-1)=n,
∴bn=(-1)n$\frac{2n+1}{{a}_{n}•{a}_{n+1}}$=(-1)n•$\frac{2n+1}{n(n+1)}$=(-1)n•($\frac{1}{n}$+$\frac{1}{n+1}$),
数列{bn}的前n项和Tn=-(1+$\frac{1}{2}$)+($\frac{1}{2}$+$\frac{1}{3}$)-($\frac{1}{3}$+$\frac{1}{4}$)+…+(-1)n•($\frac{1}{n}$+$\frac{1}{n+1}$),
当n为偶数时,Tn=-1+$\frac{1}{n+1}$,
当n为奇数时,Tn=-1+$\frac{1}{n}$-($\frac{1}{n}$+$\frac{1}{n+1}$)=-1-$\frac{1}{n+1}$,
综上所述Tn=-1+$\frac{(-1)^{n}}{n+1}$,
故答案为:-1+$\frac{(-1)^{n}}{n+1}$.
点评 本题考查了数列的递推公式关系式,和数列的通项公式,以及数列的前n项和,属于中档题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:选择题
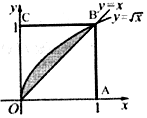 向如图所示的正方形OABC内任意投一点,该点恰好落在图中阴影部分的概率为( )
向如图所示的正方形OABC内任意投一点,该点恰好落在图中阴影部分的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{{2^{n+1}}-n-2}}{2^n}$ | B. | $\frac{{{2^{n+1}}-n-2}}{{{2^{n+1}}}}$ | C. | $\frac{{{2^{n+1}}-n-1}}{2^n}$ | D. | $\frac{{{2^{n+1}}-n-1}}{{{2^{n+1}}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ω=1 | B. | ω=2 | C. | ω=$\frac{1}{2}$ | D. | ω=$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四面体ABCD中,CA=CD,AD⊥BD,点E,F分别是AB,AD的中点,
如图,在四面体ABCD中,CA=CD,AD⊥BD,点E,F分别是AB,AD的中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com