
|
|
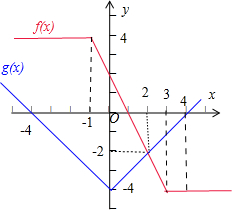 解:(Ⅰ)∵函数f(x)=|x-3|-|x+1|=
解:(Ⅰ)∵函数f(x)=|x-3|-|x+1|=
|
|
| 3 |
| 2 |


科目:高中数学 来源: 题型:
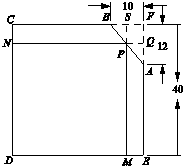 有一块铁皮零件,它的形状是由边长为40cm的正方形CDEF截去一个三角形ABF所得的五边形ABCDE,其中AF长等于12cm,BF长等于10cm,如图所示.现在需要截取矩形铁皮,使得矩形相邻两边在CD,DE上.请问如何截取,可以使得到的矩形面积最大?(图中单位:cm)
有一块铁皮零件,它的形状是由边长为40cm的正方形CDEF截去一个三角形ABF所得的五边形ABCDE,其中AF长等于12cm,BF长等于10cm,如图所示.现在需要截取矩形铁皮,使得矩形相邻两边在CD,DE上.请问如何截取,可以使得到的矩形面积最大?(图中单位:cm)查看答案和解析>>
科目:高中数学 来源: 题型:
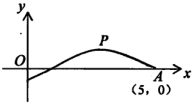 如图,是函数y=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象的一段,O坐标原点,P(3,1)是该段图象的最高点,A(5,0)是该段图象与x轴的一个交点,则此函数的解析式为
如图,是函数y=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象的一段,O坐标原点,P(3,1)是该段图象的最高点,A(5,0)是该段图象与x轴的一个交点,则此函数的解析式为查看答案和解析>>
科目:高中数学 来源: 题型:
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | [160,165) | 5 | 0.050 |
| 第二组 | [165,170) | a | 0.350 |
| 第三组 | [170,175) | 30 | b |
| 第四组 | [175,180) | c | 0.200 |
| 第五组 | [180,185] | 10 | 0.100 |
| 合计 | 100 | 1.00 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com