
如下图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.

(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1;
(3)求异面直线AC1与B1C所成角的余弦值.
(1)先证明AC⊥平面BCC1B1,再根据性质即可证明
(2)先证明DE∥AC1,再根据线面平行的判定定理证明
(3)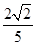
【解析】
试题分析:(1)在直三棱柱ABC-A1B1C1中,底面三边长AC=3,BC=4,AB=5,
∴AC⊥BC.又∵C1C⊥AC.∴AC⊥平面BCC1B1.
∵BC1?平面BCC1B,∴AC⊥BC1.
(2)设CB1与C1B的交点为E,连接DE,又四边形BCC1B1为正方形.
∵D是AB的中点,E是BC1的中点,∴DE∥AC1.
∵DE?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1.
(3)∵DE∥AC1,∴∠CED为AC1与B1C所成的角.
在△CED中,ED=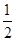 AC1=
AC1=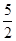 ,CD=
,CD=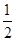 AB=
AB=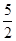 ,CE=
,CE=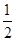 CB1=2
CB1=2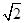 ,
,
∴cos∠CED= =
=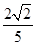 .
.
∴异面直线AC1与B1C所成角的余弦值为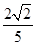 .
.
考点:本小题主要考查线线垂直、线面平行的判定和两条异面直线所成的角的计算,考查学生的空间想象能力和运算求解能力.
点评:解决此类问题,要准确应用相应的判定定理和性质定理并注意相互转化,求解两条异面直线的夹角问题时,要注意夹角的取值范围.


科目:高中数学 来源:必修二训练数学北师版 北师版 题型:022
如下图所示,在直三棱柱ABC-A1B1C1中,AB=BC=![]() ,BB1=2,∠ABC=90°,E、F分别为AA1、C1B1的中点,沿棱柱的表面从E点到F点的最短路径的长度为________.
,BB1=2,∠ABC=90°,E、F分别为AA1、C1B1的中点,沿棱柱的表面从E点到F点的最短路径的长度为________.

查看答案和解析>>
科目:高中数学 来源:山东省费县2009届高三上学期期中考试(数学文) 题型:044
如下图所示:在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.

(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1;
(3)求异面直线AC1与B1C所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年山东苍山期末文)(12分)
如下图所示:在直三棱柱ABC―A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点。

(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1;
(3)求异面直线AC1与B1C所成角的余弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com