
分析 (1)当m=2,且x<0时,$f(x)=-x+\frac{2}{x}-2$为减函数.运用单调性的定义证明,分取值、作差、变形和定符号、下结论;
(2)由题意可得(2x)2-2•2x+m>0,即m>2•2x-(2x)2,运用配方法求出右边的最大值,可得m的范围;
(3)由f(x)=0可得x|x|-2x+m=0(x≠0),变为m=-x|x|+2x(x≠0),令g(x)=-x|x|+2x(x≠0),作出y=g(x)和y=m的图象,平移即可得到所求零点个数.
解答 解:(1)当m=2,且x<0时,$f(x)=-x+\frac{2}{x}-2$为减函数…(1分)
证明:设x1<x2<0,则$f({x_1})-f({x_2})=-{x_1}+\frac{2}{x_1}-2-(-{x_2}+\frac{2}{x_2}-2)$
=$({x_2}-{x_1})+(\frac{2}{x_1}-\frac{2}{x_2})$=$({x_2}-{x_1})+\frac{{2({x_2}-{x_1})}}{{{x_1}{x_2}}}$…(2分)
=$({x_2}-{x_1})(1+\frac{2}{{{x_1}{x_2}}})$…(3分)
又x1<x2<0,所以x2-x1>0,x1x2>0,所以$({x_2}-{x_1})(1+\frac{2}{{{x_1}{x_2}}})>0$,
所以f(x1)-f(x2)>0,所以f(x1)>f(x2),
故当m=2,且x<0时,$f(x)=-x+\frac{2}{x}-2$为减函数…(4分)
(2)由f(2x)>0得$|{2^x}|+\frac{m}{2^x}-2>0$,变形为(2x)2-2•2x+m>0…(5分)
即m>2•2x-(2x)2…(6分)
而2•2x-(2x)2=-(2x-1)2+1,当2x=1即x=0时(2•2x-(2x)2)max=1…(7分)
所以m>1…(8分)
(3)由f(x)=0可得x|x|-2x+m=0(x≠0),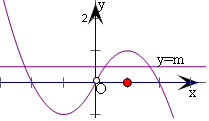
变为m=-x|x|+2x(x≠0)
令$g(x)=2x-x|x|=\left\{\begin{array}{l}-{x^2}+2x,x>0\\{x^2}+2x,x<0\end{array}\right.$…(10分
作y=g(x)的图象及直线y=m,由图象可得:
当m>1或m<-1时,f(x)有1个零点;
当m=1或m=0或m=-1时,f(x)有2个零点;
当0<m<1或-1<m<0时,f(x)有3个零点…(12分)
点评 本题考查函数的单调性的判断和证明,注意运用定义法,考查不等式恒成立问题的解法,注意运用参数分离法,同时考查函数的零点个数问题,注意运用数形结合思想方法,考查化简运算作图能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(x≠±3) | B. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(x≠±5) | ||
| C. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1(x≠±3) | D. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1(x≠±5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
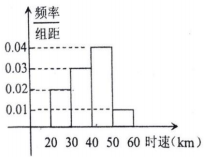 太原市某时段100辆汽车通过祥云桥时,时速的频率分布直方图如图所示,则时速在[30,40]的汽车约有( )
太原市某时段100辆汽车通过祥云桥时,时速的频率分布直方图如图所示,则时速在[30,40]的汽车约有( )| A. | 30辆 | B. | 35辆 | C. | 40辆 | D. | 50辆 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{15}{4}$ | B. | $\frac{13}{4}$ | C. | $\frac{12}{5}$ | D. | $\frac{13}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com