
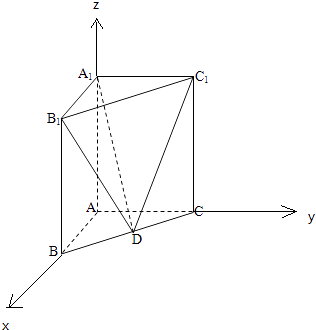
【题目】如图,在直三棱柱ABC﹣A1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3.D是线段BC的中点. 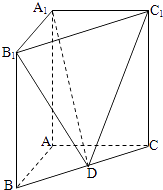
(1)求直线DB1与平面A1C1D所成角的正弦值;
(2)求二面角B1﹣A1D﹣C1的大小的余弦值.
【答案】
(1)解:因为在直三棱柱ABC﹣A1B1C1中,AB⊥AC,
所以分别以AB、AC、AA1所在的直线为x轴、y轴、z轴,建立空间直角坐标系,
则A(0,0,0),B(2,0,0),C(0,4,0),A1(0,0,3),B1(2,0,3),C1(0,4,3),
因为D是BC的中点,所以D(1,2,0),
因为 ![]() ,设平面A1C1D的法向量
,设平面A1C1D的法向量 ![]() ,
,
则 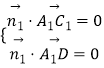 ,即
,即 ![]() ,取
,取 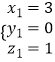 ,
,
所以平面A1C1D的法向量 ![]() ,而
,而 ![]() ,
,
所以 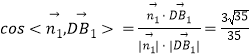 ,
,
所以直线DB1与平面A1C1D所成角的正弦值为 ![]()
(2)解: ![]() ,
, ![]() ,
,
设平面B1A1D的法向量 ![]() ,
,
则 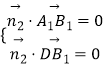 ,即
,即 ![]() ,
,
取 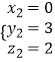 ,平面B1A1D的法向量
,平面B1A1D的法向量 ![]() ,
,
所以 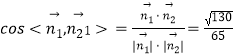 ,
,
二面角B1﹣A1D﹣C1的大小的余弦值 ![]() .
.
【解析】(1)分别以AB、AC、AA1所在的直线为x轴、y轴、z轴,建立空间直角坐标系,利用向量法能求出直线DB1与平面A1C1D所成角的正弦值.(2)求出平面B1A1D的法向量和平面B1A1D的法向量,利用向量法能求出二面角B1﹣A1D﹣C1的大小的余弦值.
【考点精析】根据题目的已知条件,利用空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则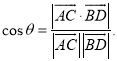 .
.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
【题目】某高校共有学生15 000人,其中男生10 500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间(单位:h)的样本数据.

(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].估计该校学生每周平均体育运动时间超过4 h的概率.
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4 h,请完成下面的2×2列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”?
男生 | 女生 | 总计 | |
每周平均体育运动时间不超过4h | |||
每周平均体育运动时间超过4h | |||
总计 |
附:
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究变量![]() ,
,![]() 得到一组样本数据,进行回归分析,有以下结论
得到一组样本数据,进行回归分析,有以下结论
①残差平方和越小的模型,拟合的效果越好;
②用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小说明拟合效果越好;
越小说明拟合效果越好;
③在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,预报变量
每增加1个单位时,预报变量![]() 平均增加0.2个单位
平均增加0.2个单位
④若变量![]() 和
和![]() 之间的相关系数为
之间的相关系数为![]() ,则变量
,则变量![]() 和
和![]() 之间的负相关很强,以上正确说法的个数是( )
之间的负相关很强,以上正确说法的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知非空集合M满足M{0,1,2,…,n}(n≥2,n∈N+).若存在非负整数k(k≤n),使得当a∈M时,均有2k﹣a∈M,则称集合M具有性质P.设具有性质P的集合M的个数为f(n).
(1)求f(2)的值;
(2)求f(n)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的一个顶点为A(2,0),离心率为
(a>b>0)的一个顶点为A(2,0),离心率为![]() .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为![]() 时,求k的值.
时,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3-3mx+n(m>0)的极大值为6,极小值为2.
(1)求实数m,n的值;
(2)求f(x)在区间[0,3]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若正整数N除以正整数m后的余数为n,则记为N≡n(mod m),例如10≡4(mod 6).下面程序框图的算法源于我国古代闻名中外的(中国剩余定理),执行该程序框图,则输出的n等于( ) 
A.17
B.16
C.15
D.13
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q是AD的中点. 
(1)若PA=PD,求证:平面PQB⊥平面PAD;
(2)若平面APD⊥平面ABCD,且PA=PD=AD=2,在线段PC上是否存在点M,使二面角M﹣BQ﹣C的大小为60°.若存在,试确定点M的位置,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com