|
|
|
定义:已知函数f(x)与g(x),若存在一条直线y=kx+b,使得对公共定义域内的任意实数均满足g(x)≤f(x)≤kx+b恒成立,其中等号在公共点处成立,则称直线y=kx+b为曲线f(x)与g(x)的“左同旁切线”.已知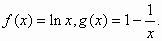
(Ⅰ)证明:直线y=x-l是f(x)与g(x)的“左同旁切线”;
(Ⅱ)设P(x1,f(x1)),Q(x2,f(x2))是函数f(x)图象上任意两点,且0<x1<x2,若存在实数x3>0,使得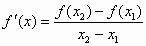 .请结合(I)中的结论证明:x1<x3<x2. .请结合(I)中的结论证明:x1<x3<x2.
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
在区间(0,1)上任意取两个实数a,b,则a+b<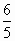 的概率为________. 的概率为________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
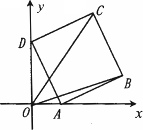
如图放置的正方形ABCD,AB=1,A,D分别在x轴、y轴的正半轴(含原点)上滑动,则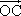 · ·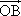 的最大值是________; 的最大值是________;
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
下表是最近十届奥运会的年份、届别、主办国,以及主办国在上届获得的金牌数、当届获得的金牌数的统计数据:
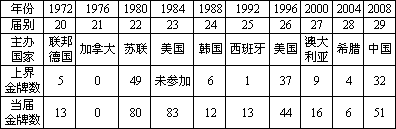
某体育爱好组织,利用上表研究所获金牌数与主办奥运会之间的关系,求出主办国在上届所获金牌数(设为x)与在当届所获金牌数(设为y)之间的线性回归方程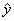 = =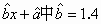 ,在2008年第29届北京奥运会上英国获得19块金牌,则据此线性回归方程估计在2012年第30届伦敦奥运会上英国将获得的金牌数为(所有金牌数精确到整数) ,在2008年第29届北京奥运会上英国获得19块金牌,则据此线性回归方程估计在2012年第30届伦敦奥运会上英国将获得的金牌数为(所有金牌数精确到整数)
|
| [ ] |
A. |
29块
|
B. |
30块
|
C. |
31块
|
D. |
32块
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
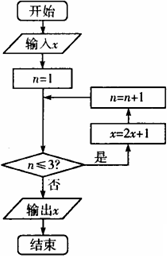
已知实数x∈[3,17],执行如图所示的程序框图,则输出的x不小于87的概率为________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设全集U={x∈Z||x|<3},A={x∈Z|x(x-3)<0},B={-2,-1,2},则A∪(CUB)=
|
| [ ] |
A. |
{1}
|
B. |
{2}
|
C. |
{0,1,2}
|
D. |
{1,2}
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知a,b均为单位向量,则“ ”是“a+b=( ”是“a+b=( )”的 )”的
|
| [ ] |
A. |
充分不必要条件
|
B. |
必要不充分条件
|
C. |
充要条件
|
D. |
既不充分也不必要条件
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
化简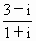 的结果为 的结果为
|
| [ ] |
A. |
1+2i
|
B. |
1–2i
|
C. |
2+i
|
D. |
2–i
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,F,G分别是PD,PC,BC的中点.
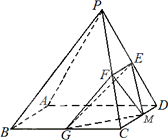
(Ⅰ)求平面EFG⊥平面PAD;
(Ⅱ)若M是线段CD上一点,求三棱锥M-EFG的体积.
|
|
|
查看答案和解析>>
