练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）= （x∈R），e是自然对数的底．
    （1）计算f（ln2）的值；
    （2）证明函数f（x）是奇函数．

    【答案】
    （1）解：f（ln2）= =
    （2）证明：函数的定义域为R．

    f（﹣x）= =﹣ =﹣f（x），

    ∴函数f（x）是奇函数


    【解析】（1）直接代入计算f（ln2）的值；（2）利用奇函数的定义证明函数f（x）是奇函数．
    【考点精析】本题主要考查了函数奇偶性的性质和函数的值的相关知识点，需要掌握在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇；函数值的求法：①配方法(二次或四次)；②“判别式法”；③反函数法；④换元法；⑤不等式法；⑥函数的单调性法才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，AD∥BC，AB⊥AD，AB⊥PA，BC=2AB=2AD=4BE，平面PAB⊥平面ABCD，
    （Ⅰ）求证：平面PED⊥平面PAC；
    （Ⅱ）若直线PE与平面PAC所成的角的正弦值为 ，求二面角A﹣PC﹣D的平面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在数列{an}中，a1＝1，an＋1＝2an＋2n.

    (1)设bn＝.证明：数列{bn}是等差数列；

    (2)求数列{an}的前n项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，直线： ，椭圆： ， 、分别为椭圆的左、右焦点．

    （1）当直线过右焦点时，求直线的方程；

    （2）设直线与椭圆交于， 两点， ， 的重心分别为， ，若原点在以线段为直径的圆内，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三棱柱中，侧棱垂直于底面， ， ， 是棱的中点.

    （Ⅰ）证明：平面⊥平面；

    （Ⅱ）求异面直线与所成角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于无穷数列，记，若数列满足：“存在，使得只要（且），必有”，则称数列具有性质.

    （Ⅰ）若数列满足判断数列是否具有性质？是否具有性质？

    （Ⅱ）求证：“是有限集”是“数列具有性质”的必要不充分条件；

    （Ⅲ）已知是各项为正整数的数列，且既具有性质，又具有性质，求证：存在整数，使得是等差数列.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左右焦点分别为，点为椭圆上一点. 的重心为，内心为，且，则该椭圆的离心率为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

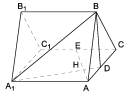
    【题目】如图，正三棱柱所有棱长都是2，D棱AC的中点，E是棱的中点，AE交于点H.

    （1）求证：平面；

    （2）求二面角的余弦值；

    （3）求点到平面的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列4个命题，其中正确的命题序号为（ ）
    ①|x+ |的最小值是2 ② 的最小值是2 ③log2x+logx2的最小值是2 ④3x+3﹣x的最小值是2．
    A.①②③
    B.①②④
    C.②③④
    D.①③④

    查看答案和解析>>

    同步练习册答案