
【题目】已知函数![]() .
.
(1)若![]() 是偶函数,求
是偶函数,求![]() 的值;
的值;
(2)设函数![]() ,当
,当![]() 时,
时,![]() 有且只有一个实数根,求
有且只有一个实数根,求![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不相等的实数根
上有两个不相等的实数根![]() ,
,![]() ,证明:
,证明:![]() .
.
 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】某种热饮需用开水冲泡,其基本操作流程如下:①先将水加热到100![]() ,水温
,水温![]() 与时间
与时间![]() 近似满足一次函数关系;②用开水将热饮冲泡后在室温下放置,温度
近似满足一次函数关系;②用开水将热饮冲泡后在室温下放置,温度![]() 与时间
与时间![]() 近似满足函数的关系式为
近似满足函数的关系式为 ![]() (
(![]() 为常数), 通常这种热饮在40
为常数), 通常这种热饮在40![]() 时,口感最佳,某天室温为
时,口感最佳,某天室温为![]() 时,冲泡热饮的部分数据如图所示,那么按上述流程冲泡一杯热饮,并在口感最佳时饮用,最少需要的时间为
时,冲泡热饮的部分数据如图所示,那么按上述流程冲泡一杯热饮,并在口感最佳时饮用,最少需要的时间为
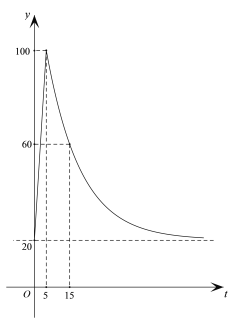
A. 35![]() B. 30
B. 30![]()
C. 25![]() D. 20
D. 20![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次活动中,有5名幸运之星.这5名幸运之星可获得![]() 、
、![]() 两种奖品中的一种,并规定:每个人通过抛掷一枚质地均为的骰子决定自己最终获得哪一种奖品(骰子的六个面上的点数分别为1点、2点、3点、4点、5点、6点),抛掷点数小于3的获得
两种奖品中的一种,并规定:每个人通过抛掷一枚质地均为的骰子决定自己最终获得哪一种奖品(骰子的六个面上的点数分别为1点、2点、3点、4点、5点、6点),抛掷点数小于3的获得![]() 奖品,抛掷点数不小于3的获得
奖品,抛掷点数不小于3的获得![]() 奖品.
奖品.
(1)求这5名幸运之星中获得![]() 奖品的人数大于获得
奖品的人数大于获得![]() 奖品的人数的概率;
奖品的人数的概率;
(2)设![]() 、
、![]() 分别为获得
分别为获得![]() 、
、![]() 两种奖品的人数,并记
两种奖品的人数,并记![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
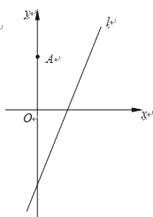
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.
(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】渔民出海打鱼,为了保证获得的鱼新鲜,鱼被打上岸后,要在最短的时间内将其分拣、冷藏,若不及时处理,打上来的鱼很快地失去新鲜度(以鱼肉内的三甲胺量的多少来确定鱼的新鲜度.三甲胺是一种挥发性碱性氨,是氨的衍生物,它是由细菌分解产生的.三甲胺量积聚就表明鱼的新鲜度下降,鱼体开始变质进而腐败).已知某种鱼失去的新鲜度![]() 与其出海后时间
与其出海后时间![]() (分)满足的函数关系式为
(分)满足的函数关系式为![]() .若出海后10分钟,这种鱼失去的新鲜度为10%,出海后20分钟,这种鱼失去的新鲜度为20%,那么若不及时处理,打上来的这种鱼在多长时间后开始失去全部新鲜度(已知
.若出海后10分钟,这种鱼失去的新鲜度为10%,出海后20分钟,这种鱼失去的新鲜度为20%,那么若不及时处理,打上来的这种鱼在多长时间后开始失去全部新鲜度(已知![]() ,结果取整数)( )
,结果取整数)( )
A.33分钟B.40分钟C.43分钟D.50分钟
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,如图所示,斜率为
,如图所示,斜率为![]() 且不过原点的直线
且不过原点的直线![]() 交椭圆
交椭圆![]() 于两点
于两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,射线
,射线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求![]() 的最小值;
的最小值;
(2)若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的有( )
①在回归分析中,可以借助散点图判断两个变量是否呈线性相关关系.
②在回归分析中,可以通过残差图发现原始数据中的可疑数据,残差平方和越小,模型的拟合效果越好.
③在回归分析模型中,相关系数的绝对值越大,说明模型的拟合效果越好.
④在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,预报变量
每增加1个单位时,预报变量![]() 增加0.1个单位.
增加0.1个单位.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班有男生27名,女生18名,用分层抽样的方法从该班中抽取5名学生去敬老院参加献爱心活动.
(1)求从该班男生、女生中分别抽取的人数;
(2)为协助敬老院做好卫生清扫工作,从参加活动的5名学生中随机抽取2名,求这2名学生均为女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com