
【题目】在三棱锥![]() 中,底面
中,底面![]() 是边长为 2 的正三角形,顶点
是边长为 2 的正三角形,顶点 ![]() 在底面
在底面![]() 上的射影为
上的射影为![]() 的中心,若
的中心,若![]() 为
为![]() 的中点,且直线
的中点,且直线![]() 与底面
与底面![]() 所成角的正切值为
所成角的正切值为![]() ,则三棱锥
,则三棱锥![]() 外接球的表面积为( )
外接球的表面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以原点为圆心,单位长度为半径的圆上有两点A( ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() ). (Ⅰ)求
). (Ⅰ)求 ![]() ,
, ![]() 夹角的余弦值;
夹角的余弦值;
(Ⅱ)已知C(1,0),记∠AOC=α,∠BOC=β,求tan ![]() 的值.
的值.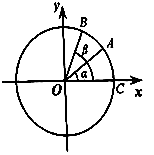
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+1(a,b为实数,a≠0,x∈R)
(1)若函数f(x)的图象过点(﹣2,1),且函数f(x)有且只有一个零点,求f(x)的表达式;
(2)在(1)的条件下,当x∈(﹣1,2)时,g(x)=f(x)﹣kx是单调函数,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
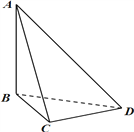
【题目】刘徽(约公元 225 年—295 年)是魏晋时期伟大的数学家,中国古典数学理论的奠基人之一,他的杰作《九章算术注》和《海岛算经》是中国宝贵的古代数学遗产. 《九章算术·商功》中有这样一段话:“斜解立方,得两壍堵. 斜解壍堵,其一为阳马,一为鳖臑.” 刘徽注:“此术臑者,背节也,或曰半阳马,其形有似鳖肘,故以名云.” 其实这里所谓的“鳖臑(biē nào)”,就是在对长方体进行分割时所产生的四个面都为直角三角形的三棱锥. 如图,在三棱锥![]() 中,
中, ![]() 垂直于平面
垂直于平面![]() ,
, ![]() 垂直于
垂直于![]() ,且
,且 ![]() ,则三棱锥
,则三棱锥![]() 的外接球的球面面积为__________.
的外接球的球面面积为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(2,0)及圆C:x2+y2﹣6x+4y+4=0.
(1)设过P直线l1与圆C交于M、N两点,当|MN|=4时,求以MN为直径的圆Q的方程;
(2)设直线ax﹣y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l2垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E﹣ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,且AB=4,BC=CD=ED=EA=2. 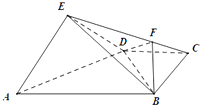
(1)求二面角E﹣AB﹣D的正切值;
(2)在线段CE上是否存在一点F,使得平面EDC⊥平面BDF?若存在,求 ![]() 的值,若不存在请说明理由.
的值,若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com