
【题目】(12分)为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ,σ2).
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在(μ–3σ,μ+3σ)之外的零件数,求P(X≥1)及X的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在(μ–3σ,μ+3σ)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() ,
,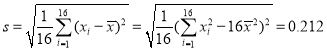 ,其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
,其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
用样本平均数![]() 作为μ的估计值
作为μ的估计值![]() ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计μ和σ(精确到0.01).
之外的数据,用剩下的数据估计μ和σ(精确到0.01).
附:若随机变量Z服从正态分布N(μ,σ2),则P(μ–3σ<Z<μ+3σ)=0.997 4,0.997 416≈0.959 2,![]() .
.
【答案】(1)![]() 的数学期望为
的数学期望为![]()
(2)详见解析
【解析】(1)抽取的一个零件的尺寸在![]() 之内的概率为0.9974,从而零件的尺寸在
之内的概率为0.9974,从而零件的尺寸在![]() 之外的概率为0.0026,故
之外的概率为0.0026,故![]() .因此
.因此
![]() .
.
![]() 的数学期望为
的数学期望为![]() .
.
(2)(i)如果生产状态正常,一个零件尺寸在![]() 之外的概率只有0.0026,一天内抽取的16个零件中,出现尺寸在
之外的概率只有0.0026,一天内抽取的16个零件中,出现尺寸在![]() 之外的零件的概率只有0.0408,发生的概率很小.因此一旦发生这种情况,就有理由认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查,可见上述监控生产过程的方法是合理的.
之外的零件的概率只有0.0408,发生的概率很小.因此一旦发生这种情况,就有理由认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查,可见上述监控生产过程的方法是合理的.
(ii)由![]() ,得
,得![]() 的估计值为
的估计值为![]() ,
,![]() 的估计值为
的估计值为![]() ,由样本数据可以看出有一个零件的尺寸在
,由样本数据可以看出有一个零件的尺寸在![]() 之外,因此需对当天的生产过程进行检查.
之外,因此需对当天的生产过程进行检查.
剔除![]() 之外的数据9.22,剩下数据的平均数为
之外的数据9.22,剩下数据的平均数为![]() ,因此
,因此![]() 的估计值为10.02.
的估计值为10.02.
![]() ,剔除
,剔除![]() 之外的数据9.22,剩下数据的样本方差为
之外的数据9.22,剩下数据的样本方差为![]() ,
,
因此![]() 的估计值为
的估计值为![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知θ为向量 ![]() 与
与 ![]() 的夹角,|
的夹角,| ![]() |=2,|
|=2,| ![]() |=1,关于x的一元二次方程x2﹣|
|=1,关于x的一元二次方程x2﹣| ![]() |x+
|x+ ![]()
![]() =0有实根.
=0有实根.
(Ⅰ)求θ的取值范围;
(Ⅱ)在(Ⅰ)的条件下,求函数f(θ)=sin(2θ+ ![]() )的最值及对应的θ的值.
)的最值及对应的θ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是
是![]() 上的动点,
上的动点, ![]() .
.
(Ⅰ)若点![]() 是
是![]() 中点,证明:平面
中点,证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)判断点![]() 到平面
到平面![]() 的距离是否为定值?若是,求出定值;若不是,请说明理由.
的距离是否为定值?若是,求出定值;若不是,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某鲜花店根据以往某品种鲜花的销售记录,绘制出日销售量的频率分布直方图,如图所示.将日销售量落入各组区间的频率视为概率,且假设每天的销售量相互独立.

(1)求在未来的连续4天中,有2天的日销售量低于100枝且另外2天不低于150枝的概率;
(2)用![]() 表示在未来4天里日销售量不低于100枝的天数,求随机变量
表示在未来4天里日销售量不低于100枝的天数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 和抛物线
和抛物线![]() :
: ![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)已知直线![]() 和圆
和圆![]() 相切,与抛物线
相切,与抛物线![]() 交于
交于![]() 两点,且满足
两点,且满足![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)过抛物线![]() 上一点
上一点![]() 作两直线
作两直线![]() 和圆
和圆![]() 相切,且分别交抛物线
相切,且分别交抛物线![]() 于
于![]() 两点,若直线
两点,若直线![]() 的斜率为
的斜率为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个四棱锥底面为正方形,顶点在底面的射影为正方形的中心,且该四棱锥的体积为9,当其外接球表面积最小时,它的高为( )
A.3
B.2 ![]()
C.2 ![]()
D.3 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题: 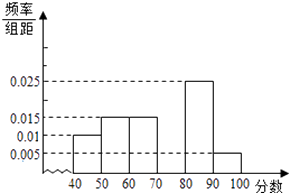
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是[40,50)和[90,100]的学生中选两人,求他们在同一分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一直线l过直线l1:3x﹣y=3和直线l2:x﹣2y=2的交点P,且与直线l3:x﹣y+1=0垂直.
(1)求直线l的方程;
(2)若直线l与圆心在x正半轴上的半径为 ![]() 的圆C相切,求圆C的标准方程.
的圆C相切,求圆C的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax﹣(k﹣1)a﹣x(a>0且a≠1)是定义域为R的奇函数.
(1)求k值;
(2)若f(1)= ![]() ,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值为﹣2,求m的值.
,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值为﹣2,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com