
 △ABC中,AD是BC边上中线,E为AD上一点,BE的延长线交AC于F,交AB的平行线CG于G.
△ABC中,AD是BC边上中线,E为AD上一点,BE的延长线交AC于F,交AB的平行线CG于G.分析 (1)证明△ABF∽△CGF,利用AC=8,BG=16,AF=3,即可求BF的长;
(2)过点C作CI∥AB,交AD的延长线于点I,过点C作CH∥BF交DI于点H.首先证明△ABD≌△ICD,△EBD≌△HCD,从而可证得BE=HC,AH=EI,然后再证明△AEF∽△AHC,从而得到:$\frac{EF}{GH}=\frac{AE}{AH}=\frac{AE}{EI}$,然后证明△ABE∽△IGE,可知$\frac{BE}{EG}=\frac{AE}{EI}$,从而得到$\frac{EF}{HC}=\frac{BE}{EG}$,根据BE=HC,可得到$\frac{EF}{BE}=\frac{BE}{EG}$,从而可证得BE2=EF•EG.
解答 (1)解:∵AB∥CG,
∴△ABF∽△CGF,
∴$\frac{AF}{CF}$=$\frac{BF}{GF}$,
∵AC=8,BG=16,AF=3,
∴$\frac{3}{5}=\frac{BF}{16-BF}$,
∴BF=6;
(2)证明:如图所示,过点C作CI∥AB,交AD的延长线于点I,过点C作CH∥BF交DI于点H.
∵AB∥CI,
∴∠BAD=∠CID.
在△ABD和△ICD中,$\left\{\begin{array}{l}{∠BAD=∠CID}\\{∠ADB=∠IDC}\\{DB=DC}\end{array}\right.$,
∴△ABD≌△ICD.
∴AD=DI.
同理:△EBD≌△HCD.
∴ED=HD,BE=HC.
∴AD+DH=DI+ED,即AH=EI.
∵EF∥HC,
∴△AEF∽△AHC.
∴$\frac{EF}{GH}=\frac{AE}{AH}=\frac{AE}{EI}$.
∵AB∥GI,
∴△ABE∽△IGE.
∴$\frac{BE}{EG}=\frac{AE}{EI}$.
∴$\frac{EF}{HC}=\frac{BE}{EG}$.
又∵BE=HC,
∴$\frac{EF}{BE}=\frac{BE}{EG}$.
∴BE2=EF•EG.
点评 本题主要考查的是相似三角形的性质和判定、全等三角形的性质和判定,利用全等三角形的性质证得AH=EI,从而得到$\frac{EF}{GH}=\frac{AE}{AH}=\frac{AE}{EI}$是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
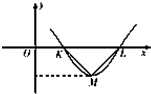 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,$\overrightarrow{MK}•\overrightarrow{ML}$=0,|KL|=1,|ML|=$\frac{{\sqrt{2}}}{2}$,则$f(\frac{1}{6})$的值为( )
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,$\overrightarrow{MK}•\overrightarrow{ML}$=0,|KL|=1,|ML|=$\frac{{\sqrt{2}}}{2}$,则$f(\frac{1}{6})$的值为( )| A. | $-\frac{{\sqrt{3}}}{4}$ | B. | $-\frac{1}{4}$ | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com