
【题目】某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:![]() ):男生成绩在175
):男生成绩在175![]() 以上(包括175
以上(包括175![]() )定义为“合格”,成绩在175
)定义为“合格”,成绩在175![]() 以下(不包括175
以下(不包括175![]() )定义为“不合格”.女生成绩在165
)定义为“不合格”.女生成绩在165![]() 以上(包括165
以上(包括165![]() )定义为“合格”,成绩在165
)定义为“合格”,成绩在165![]() 以下(不包括165
以下(不包括165![]() )定义为“不合格”.
)定义为“不合格”.
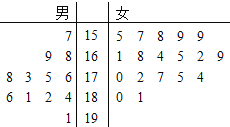
(1)求五年一班的女生立定跳远成绩的中位数;
(2)在五年一班的男生中任意选取3人,求至少有2人的成绩是合格的概率;
(3)若从五年一班成绩“合格”的学生中选取2人参加复试,用![]() 表示其中男生的人数,写出
表示其中男生的人数,写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
【答案】(1)166.5cm (2) ![]() (3)见解析
(3)见解析
【解析】
(1)按照中位数的定义,可以根据茎叶图得到五年一班的女生立定跳远成绩的中位数;
(2) 男生中任意选取3人,至少有2人的成绩是合格,包括两个事件:一个为事件![]() :“仅有两人的成绩合格”,另一个为事件
:“仅有两人的成绩合格”,另一个为事件![]() :“有三人的成绩合格”,所以至少有两人的成绩是合格的概率:
:“有三人的成绩合格”,所以至少有两人的成绩是合格的概率:![]() ,分别求出
,分别求出![]() ,最后求出
,最后求出![]() ;
;
(3) 因为合格的人共有18人,其中有女生有10人合格,男生有8人合格,依题意,![]() 的取值为0,1,2,分别求出
的取值为0,1,2,分别求出![]() 的值,最后列出
的值,最后列出![]() 的分布列和计算出
的分布列和计算出![]() 的数学期望.
的数学期望.
解:(1)由茎叶图得五年一班的女生立定跳远成绩的中位数为![]()
(2)设“仅有两人的成绩合格”为事件![]() ,“有三人的成绩合格”为事件
,“有三人的成绩合格”为事件![]() ,
,
至少有两人的成绩是合格的概率:![]() ,
,
又男生共12人,其中有8人合格,从而![]() ,
,
![]() ,所以
,所以![]() .
.
(3)因为合格的人共有18人,其中有女生有10人合格,男生有8人合格,
依题意,![]() 的取值为0,1,2,
的取值为0,1,2,
则![]() ,
,
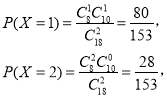
因此,X的分布列如下:
| 0 | 1 | 2 |
|
|
|
|
![]() (人).
(人).
或是,因为![]() 服从超几何分布,所以
服从超几何分布,所以![]() (人).
(人).


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,椭圆
,椭圆![]() 上任意一点到椭圆两个焦点的距离之和为6.
上任意一点到椭圆两个焦点的距离之和为6.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]()
![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() (0,1),且
(0,1),且![]() =
=![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣2)ex﹣![]() +
+![]() x,其中
x,其中![]() ∈R,e是自然对数的底数.
∈R,e是自然对数的底数.
(1)当![]() >0时,讨论函数f(x)在(1,+∞)上的单调性;
>0时,讨论函数f(x)在(1,+∞)上的单调性;
(2)若函数g(x)=f![]() (x)+2﹣
(x)+2﹣![]() ,证明:使g(x)≥0在
,证明:使g(x)≥0在![]() 上恒成立的实数a能取到的最大整数值为1.
上恒成立的实数a能取到的最大整数值为1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其图象关于直线
,其图象关于直线![]() 对称,为了得到函数
对称,为了得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象上的所有点( )
的图象上的所有点( )
A.先向左平移![]() 个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
B.先向右平移![]() 个单位长度,再把所得各点横坐标缩短为原来的
个单位长度,再把所得各点横坐标缩短为原来的![]() ,纵坐标保持不变
,纵坐标保持不变
C.先向右平移![]() 个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
D.先向左平移![]() 个单位长度,再把所得各点横坐标缩短为原来的
个单位长度,再把所得各点横坐标缩短为原来的![]() ,纵坐标保持不变
,纵坐标保持不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的各项都是正数,若对于任意的正整数
的各项都是正数,若对于任意的正整数![]() ,存在
,存在![]() ,使得
,使得![]() 、
、![]() 、
、![]() 成等比数列,则称函数
成等比数列,则称函数![]() 为“
为“![]() 型”数列.
型”数列.
(1)若![]() 是“
是“![]() 型”数列,且
型”数列,且![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)若![]() 是“
是“![]() 型”数列,且
型”数列,且![]() ,
,![]() ,求
,求![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若![]() 既是“
既是“![]() 型”数列,又是“
型”数列,又是“![]() 型”数列,求证:数列
型”数列,求证:数列![]() 是等比数列.
是等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,射线![]() 和
和![]() 均为笔直的公路,扇形
均为笔直的公路,扇形![]() 区域(含边界)是一蔬菜种植园,其中
区域(含边界)是一蔬菜种植园,其中![]() 、
、![]() 分别在射线
分别在射线![]() 和
和![]() 上.经测量得,扇形
上.经测量得,扇形![]() 的圆心角(即
的圆心角(即![]() )为
)为![]() 、半径为1千米.为了方便菜农经营,打算在扇形
、半径为1千米.为了方便菜农经营,打算在扇形![]() 区域外修建一条公路
区域外修建一条公路![]() ,分别与射线
,分别与射线![]() 、
、![]() 交于
交于![]() 、
、![]() 两点,并要求
两点,并要求![]() 与扇形弧
与扇形弧![]() 相切于点
相切于点![]() .设
.设![]() (单位:弧度),假设所有公路的宽度均忽略不计.
(单位:弧度),假设所有公路的宽度均忽略不计.
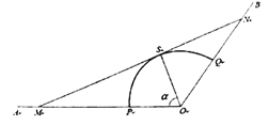
(1)试将公路![]() 的长度表示为
的长度表示为![]() 的函数,并写出
的函数,并写出![]() 的取值范围;
的取值范围;
(2)试确定![]() 的值,使得公路
的值,使得公路![]() 的长度最小,并求出其最小值.
的长度最小,并求出其最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
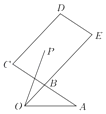
【题目】如图,B是AC的中点,![]() ,P是平行四边形BCDE内(含边界)的一点,且
,P是平行四边形BCDE内(含边界)的一点,且![]() .有以下结论:
.有以下结论:
①当x=0时,y∈[2,3];
②当P是线段CE的中点时,![]() ;
;
③若x+y为定值1,则在平面直角坐标系中,点P的轨迹是一条线段;
④x﹣y的最大值为﹣1;
其中你认为正确的所有结论的序号为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com