
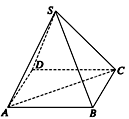
.如图所示,已知正四棱锥S—ABCD中,底面边长为a,侧棱长为![]() a.
a.
(1)求它的外接球的体积;
(2)求它的内切球的表面积.
(1)V球=![]()
![]() R3=
R3=![]()
![]() a3(2)V棱锥=
a3(2)V棱锥=![]() S底h=
S底h=![]() a2×
a2×![]() a=
a=![]()
(1)设外接球的半径为R,球心为O,则OA=OC=OS,所以O为△SAC的外心,
即△SAC的外接圆半径就是球的半径.
∵AB=BC=a,∴AC=![]() a.
a.
∵SA=SC=AC=![]() a,∴△SAC为正三角形.
a,∴△SAC为正三角形.
 由正弦定理得2R=
由正弦定理得2R=![]() ,
,
因此,R=![]() a,V球=
a,V球=![]()
![]() R3=
R3=![]()
![]() a3.
a3.
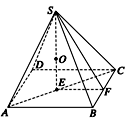
(2)设内切球半径为r,作SE⊥底面ABCD于E,
作SF⊥BC于F,连接EF,
则有SF=![]()
=![]() .
.
S△SBC=![]() BC·SF=
BC·SF=![]() a×
a×![]() a=
a=![]() a2.
a2.
S棱锥全=4S△SBC+S底=(![]() +1)a2.
+1)a2.
又SE=![]() =
=![]() =
=![]() ,
,
∴V棱锥=![]() S底h=
S底h=![]() a2×
a2×![]() a=
a=![]() .
.
∴r=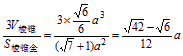 ,
,
S球=4![]() r2=
r2=![]()
![]() a2.
a2.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
 如图所示,已知正四棱柱ABCD-A1B1C1D1的底面边长为1,点E在棱AA1上,A1C∥平面EBD,截面EBD的面积为
如图所示,已知正四棱柱ABCD-A1B1C1D1的底面边长为1,点E在棱AA1上,A1C∥平面EBD,截面EBD的面积为
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)证明EF为BD1与CC1的公垂线;
(2)求点D1到平面BDE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,已知正四棱锥S—ABCD侧棱长为![]() ,底面边长为
,底面边长为![]() ,E是SA的中点,则异面直线BE与SC所成角的大小为 ( )
,E是SA的中点,则异面直线BE与SC所成角的大小为 ( )
A.90° B.60°
C.45° D.30°
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高二上期中考试理科数学试卷(解析版) 题型:选择题
如图所示,已知正四棱锥 侧棱长为
侧棱长为 ,底面边长为
,底面边长为 ,
, 是
是 的中点,则异面直线
的中点,则异面直线 与
与 所成角的大小为(
)
所成角的大小为(
)

A.  B.
B.  C.
C.
 D.
D.

查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三一轮复习质量检测理科数学 题型:选择题
如图所示,已知正四棱锥S—ABCD侧棱长为 ,底面边长为
,底面边长为 ,E是SA的中点,则异面直线BE与SC所成角的大小为
( )
,E是SA的中点,则异面直线BE与SC所成角的大小为
( )
A.90° B.60° C.45° D.30°

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com