
【题目】已知线段AB的两个端点A、B分别在x轴和y轴上滑动,且∣AB∣=2.
(1)求线段AB的中点P的轨迹C的方程;
(2)求过点M(1,2)且和轨迹C相切的直线方程.
【答案】(1)x2+y2=1(2) x=1或3x-4y+5=0
【解析】本题考查点轨迹方程的求法,两点间的距离公式的应用,体现了分类讨论的数学思想,注意考虑切线的斜率不存在的情况,这是易错点
(1)设P(x,y),由|AB|=2,且P为AB的中点,可得|OP|=1,由两点间的距离公式求得点P的轨迹方程.
(2)①当切线的斜率不存在时,由条件易得x=1符合条件;②当切线的斜率存在时,设出切线方程,由切线的性质可解得斜率k的值,用点斜式求得切线方程.
解: (1) 方法一:设P(x , y ),
∵∣AB∣=2,且P为AB的中点,
∴∣OP∣=1 ……………………2分
∴点P的轨迹方程为x2+y2=1. ……………………4分
方法二:设P(x , y ), ∵P为AB的中点,
∴A (2x , 0 ), B(0 , 2y ), ………………………2分
又∵∣AB∣=2 ∴(2x)2+(2y)2=2
化简得点P的轨迹C的方程为x2+y2=1. ……………4分
(2) ①当切线的斜率不存在时,切线方程为x=1,
由条件易得 x=1符合条件; ………………5分
②当切线的斜率存在时,设切线方程为 y-2=k(x-1) 即kx-y+2-k=0
由![]() 得k=
得k=![]() , ∴切线方程为y-2=
, ∴切线方程为y-2=![]() (x-1)
(x-1)
即 3x-4y+5=0
综上,过点M(1,2)且和轨迹C相切的直线方程为:
x=1 或3x-4y+5=0 ……………………8分


科目:高中数学 来源: 题型:
【题目】已知右焦点为F(c,0)的椭圆M: ![]() =1(a>b>0)过点
=1(a>b>0)过点 ![]() ,且椭圆M关于直线x=c对称的图形过坐标原点.
,且椭圆M关于直线x=c对称的图形过坐标原点.
(1)求椭圆M的方程;
(2)过点(4,0)且不垂直于y轴的直线与椭圆M交于P,Q两点,点Q关于x轴的对称原点为E,证明:直线PE与x轴的交点为F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为![]() 元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.若使租赁公司的月收益最大,每辆车的月租金应该定为__________.
元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.若使租赁公司的月收益最大,每辆车的月租金应该定为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是圆柱的母线,
是圆柱的母线, ![]() 是
是![]() 的直径,
的直径, ![]() 是底面圆周上异于
是底面圆周上异于![]() 的任意一点,
的任意一点, ![]() ,
, ![]() .
.
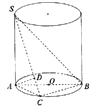
(1)求证: ![]()
(2)当三棱锥![]() 的体积最大时,求
的体积最大时,求![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(3)![]() 上是否存在一点
上是否存在一点![]() ,使二面角
,使二面角![]() 的平面角为45°?若存在,求出此时
的平面角为45°?若存在,求出此时![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() 的离心率为e,经过第一、三象限的渐近线的斜率为k,且e≥
的离心率为e,经过第一、三象限的渐近线的斜率为k,且e≥ ![]() k.
k.
(1)求m的取值范围;
(2)设条件p:e≥ ![]() k;条件q:m2﹣(2a+2)m+a(a+2)≤0.若p是q的必要不充分条件,求a的取值范围.
k;条件q:m2﹣(2a+2)m+a(a+2)≤0.若p是q的必要不充分条件,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )
)
(1)若![]() ,用“五点法”在给定的坐标系中,画出函数
,用“五点法”在给定的坐标系中,画出函数![]() 在[0,π]上的图象.
在[0,π]上的图象.

(2)若![]() 偶函数,求
偶函数,求![]()
(3)在(2)的前提下,将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后,再将得到的图象上各点的横坐标变为原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标变为原来的4倍,纵坐标不变,得到函数![]() 的图象,求
的图象,求![]() 在
在![]() 的单调递减区间.
的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】田忌和齐王赛马是历史上有名的故事,设齐王的三匹马分别为![]() ,田忌的三匹马分别为
,田忌的三匹马分别为![]() .三匹马各比赛一次,胜两场者为获胜.若这六匹马比赛的优劣程度可以用以下不等式表示:
.三匹马各比赛一次,胜两场者为获胜.若这六匹马比赛的优劣程度可以用以下不等式表示: ![]() .
.
(1)如果双方均不知道对方马的出场顺序,求田忌获胜的概率;
(2)为了得到更大的获胜概率,田忌预先派出探子到齐王处打探实情,得知齐王第一场必出上等马,那么,田忌应怎样安排出马的顺序,才能使自己获胜的概率最大?最大概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com