
【题目】如图,在直角梯形SABC中,∠B=∠C= ![]() ,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB.
,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB. 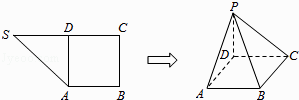
(1)求证:PD⊥平面ABCD;
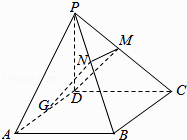
(2)已知PD=AD,PD+AD+DC=6,G是AD的中点,当线段PB取得最小值时,则在平面PBC上是否存在点F,使得FG⊥平面PBC?若存在,确定点F的位置,若不存在,请说明理由.
【答案】
(1)证明:∵PA⊥AB,AB⊥AD,PA⊥AD=A,
∴AB⊥平面PAD,
∵PD平面PAD,
∴AB⊥PD,
∵PD⊥AD,AD∩AB=A,
∴PD⊥平面ABCD
(2)解:设PD=x,则AD=x,DC=6﹣2x,
∴PB2=x2+x2+(6﹣2x)2=6(x﹣2)2+12,当且仅当x=2时,PB2取得最小值,
即PB取得最小值,
取PC的中点M,PB的中点N,
则DM⊥平面PBC,
∵四边形DMNG是平行四边形,
∴GN∥DM,
GN⊥平面PBC,
∴在平面PBC上存在点F,即PB的中点,使FG⊥平面PBC.
【解析】(1)根据线面垂直的判定定理即可证明PD⊥平面ABCD;(2)根据线面垂直的判定定理以及直线平行的性质进行证明即可.
【考点精析】本题主要考查了直线与平面垂直的判定的相关知识点,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知过抛物线 ![]() 的焦点,斜率为
的焦点,斜率为 ![]() 的直线交抛物线于
的直线交抛物线于 ![]() ,
, ![]() (
( ![]() )两点,且
)两点,且 ![]() .
.
(1)求该抛物线的方程;
(2)![]() 为坐标原点,
为坐标原点, ![]() 为抛物线上一点,若
为抛物线上一点,若 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某淘宝商城在2017年前7个月的销售额![]() (单位:万元)的数据如下表,已知
(单位:万元)的数据如下表,已知![]() 与
与![]() 具有较好的线性关系.
具有较好的线性关系. 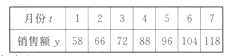
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)分析该淘宝商城2017年前7个月的销售额的变化情况,并预测该商城8月份的销售额.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
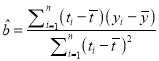 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 在区间
在区间![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,若对任意的
时,若对任意的![]() ,总存在
,总存在![]() 使
使![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 的值域为区间
的值域为区间![]() ,是否存在常数
,是否存在常数![]() ,使区间
,使区间![]() 的长度为
的长度为![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,请说明理由.(柱:区间
的值,若不存在,请说明理由.(柱:区间![]() 的长度为
的长度为![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足:![]()
(1) 证明:数列![]() 是等比数列;
是等比数列;
(2) 求使不等式![]() 成立的所有正整数m、n的值;
成立的所有正整数m、n的值;
(3) 如果常数0 < t < 3,对于任意的正整数k,都有![]() 成立,求t的取值范围.
成立,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,向量
项和,向量![]() ,
,![]() ,
,
![]() .
.
(1)若![]() ,求数列
,求数列![]() 通项公式;
通项公式;
(2)若![]() ,
,![]() .
.
①证明:数列![]() 为等差数列;
为等差数列;
②设数列![]() 满足
满足![]() ,问是否存在正整数
,问是否存在正整数![]() ,
,![]() ,且
,且![]() ,
,![]() ,使得
,使得![]() 、
、![]() 、
、![]() 成等比数列,若存在,求出
成等比数列,若存在,求出![]() 、
、![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)一个盒子里装有三张卡片,分别标记有数字![]() ,
,![]() ,
,![]() ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取![]() 次,每次抽取
次,每次抽取![]() 张,将抽取的卡片上的数字依次记为
张,将抽取的卡片上的数字依次记为![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求“抽取的卡片上的数字满足![]() ”的概率;
”的概率;
(Ⅱ)求“抽取的卡片上的数字![]() ,
,![]() ,
,![]() 不完全相同”的概率.
不完全相同”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com