
£Ø±¾Š”ĢāĀś·Ö12·Ö£©
ijŹŠĪŖĮĖ¶ŌѧɜµÄŹżĄķ£ØŹżŃ§ÓėĪļĄķ£©Ń§Ļ°ÄÜĮ¦½ųŠŠ·ÖĪö£¬“Ó10000Ćūѧɜ֊Ė껜³é³ö100Ī»Ń§ÉśµÄŹżĄķ×ŪŗĻѧĻ°ÄÜĮ¦µČ¼¶·ÖŹż(6·ÖÖĘ)×÷ĪŖŃł±¾£¬·ÖŹżĘµŹż·Ö²¼ČēĻĀ±ķ£ŗ
|
µČ¼¶µĆ·Ö |
|
|
|
|
|
|
|
ČĖŹż |
3 |
17 |
30 |
30 |
17 |
3 |
£Ø¢ń£©Čē¹ūŅŌÄÜĮ¦µČ¼¶·ÖŹż“óÓŚ4·Ö×÷ĪŖĮ¼ŗƵıź×¼£¬“ÓŃł±¾ÖŠČĪŅā³éČ”£²Ćūѧɜ£¬ĒóĒ”ÓŠ£±ĆūѧɜĪŖĮ¼ŗƵÄøÅĀŹ£»
£Ø¢ņ£©Ķ³¼Ę·½·ØÖŠ£¬Ķ¬Ņ»×鏿¾Ż³£ÓĆøĆ×éĒų¼äµÄÖŠµćÖµ£ØĄżČēĒų¼ä µÄÖŠµćÖµĪŖ1.5£©×÷ĪŖ“ś±ķ£ŗ
µÄÖŠµćÖµĪŖ1.5£©×÷ĪŖ“ś±ķ£ŗ
(¢”)¾Ż“Ė£¬¼ĘĖćÕā100ĆūѧɜŹżĄķѧĻ°ÄÜĮ¦µČ¼¶·ÖŹżµÄĘŚĶū ¼°±ź×¼²ī
¼°±ź×¼²ī (¾«Č·µ½0.1)£»
(¾«Č·µ½0.1)£»
(¢¢) Čō×ÜĢå·ž“ÓÕżĢ¬·Ö²¼,ŅŌŃł±¾¹Ą¼Ę×ÜĢå,¹Ą¼ĘøĆŹŠÕā10000Ćūѧɜ֊ŹżĄķѧĻ°ÄÜĮ¦µČ¼¶ŌŚ ·¶Ī§ÄŚµÄČĖŹż £®
·¶Ī§ÄŚµÄČĖŹż £®
£Ø¢ó£©“ÓÕā10000Ćūѧɜ֊ČĪŅā³éČ”5ĆūĶ¬Ń§£¬
ĖūĆĒŹżŃ§ÓėĪļĄķµ„æĘѧĻ°ÄÜĮ¦µČ¼¶·Ö
ŹżČēĻĀ±ķ£ŗ


£Ø¢”£©Ēė»³öÉĻ±ķŹż¾ŻµÄÉ¢µćĶ¼£»
£Ø¢¢£©Ēėøł¾ŻÉĻ±ķĢį¹©µÄŹż¾Ż£¬ÓĆ×īŠ”¶ž³Ė·ØĒó³ö ¹ŲÓŚ
¹ŲÓŚ µÄĻߊŌ»Ų¹é·½³Ģ
µÄĻߊŌ»Ų¹é·½³Ģ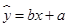 £Øø½²Īæ¼Źż¾Ż£ŗ
£Øø½²Īæ¼Źż¾Ż£ŗ £©
£©
½ā£ŗ£Ø¢ń£©Ńł±¾ÖŠ£¬Ń§ÉśĪŖĮ¼ŗƵÄČĖŹżĪŖ£²£°ČĖ£®¹Ź“ÓŃł±¾ÖŠČĪŅā³éČ”£²Ćūѧɜ£¬Ōņ½öÓŠ£±ĆūѧɜĪŖĮ¼ŗƵÄøÅĀŹĪŖ
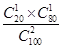 £½
£½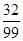 -------------2·Ö
-------------2·Ö
£Ø¢ņ£© (¢”)×ÜĢåŹż¾ŻµÄĘŚĶūŌ¼ĪŖ£ŗ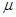 =0.5”Į0.03+1.5”Į0.17+2.5”Į0.30+3.5”Į0.30+4.5”Į0.17+5.5”Į0.03=3.0-------------4·Ö
=0.5”Į0.03+1.5”Į0.17+2.5”Į0.30+3.5”Į0.30+4.5”Į0.17+5.5”Į0.03=3.0-------------4·Ö
±ź×¼²ī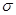 =
=
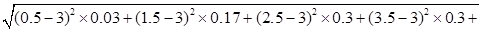
 £½
£½
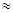 1.1---------------6·Ö
1.1---------------6·Ö
(¢¢)ÓÉÓŚ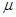 =3,
=3, 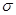
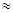 1.1
1.1
µ±x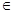
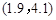 Ź±£¬¼“x
Ź±£¬¼“x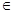 (
(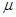 -
-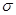 ,
,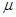 +
+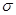 )
)
¹ŹŹżŃ§Ń§Ļ°ÄÜĮ¦µČ¼¶·ÖŹżŌŚ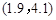 ·¶Ī§ÖŠµÄøÅĀŹ0.6826£®
·¶Ī§ÖŠµÄøÅĀŹ0.6826£®
ŹżŃ§Ń§Ļ°ÄÜĮ¦µČ¼¶ŌŚ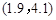 ·¶Ī§ÖŠµÄѧɜµÄČĖŹżŌ¼ĪŖ6826ČĖ£®-----------------8·Ö
·¶Ī§ÖŠµÄѧɜµÄČĖŹżŌ¼ĪŖ6826ČĖ£®-----------------8·Ö
£Ø¢ó£©
£Ø¢”£©Źż¾ŻµÄÉ¢µćĶ¼ČēĻĀĶ¼£ŗ

-------------9·Ö
£Ø¢¢£©ÉčĻߊŌ»Ų¹é·½³ĢĪŖ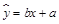 £¬Ōņ
£¬Ōņ
·½·ØŅ»: 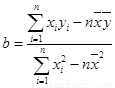 =
=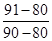 =1.1
=1.1 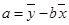 =4£1.1”Į4=-0.4
=4£1.1”Į4=-0.4
¹Ź»Ų¹éÖ±Ļß·½³ĢĪŖ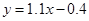 -----12·Ö
-----12·Ö
·½·Ø¶ž:

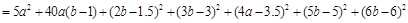
”ą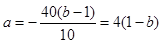 Ź±£¬
Ź±£¬
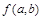 Č”µĆ×īŠ”Öµ10b
Č”µĆ×īŠ”Öµ10b -22b+12.5
-22b+12.5
¼“£¬”ą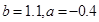 Ź±£ę£Øa£¬£ā£©Č”µĆ×īŠ”Öµ£»
Ź±£ę£Øa£¬£ā£©Č”µĆ×īŠ”Öµ£»
ĖłŅŌĻߊŌ»Ų¹é·½³ĢĪŖ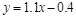 .---------12·Ö
.---------12·Ö
”¾½āĪö”æĀŌ


 ±øÕ½ÖŠæ¼ŗ®¼ŁĻµĮŠ“š°ø
±øÕ½ÖŠæ¼ŗ®¼ŁĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| 3 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| ON |
| ON |
| 5 |
| OM |
| OT |
| M1M |
| N1N |
| OP |
| OA |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
£Ø±¾Š”ĢāĀś·Ö12·Ö£©ŅŃÖŖŗÆŹż![]() £¬ĒŅ
£¬ĒŅ![]() ”£¢ŁĒó
”£¢ŁĒó![]() µÄ×ī“óÖµ¼°×īŠ”Öµ£»¢ŚĒó
µÄ×ī“óÖµ¼°×īŠ”Öµ£»¢ŚĒó![]() µÄŌŚ¶ØŅåÓņÉĻµÄµ„µ÷Ēų¼ä.
µÄŌŚ¶ØŅåÓņÉĻµÄµ„µ÷Ēų¼ä.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
£Ø2009ŗžÄĻ¾ķĪÄ£©£Ø±¾Š”ĢāĀś·Ö12·Ö£©
ĪŖĄ¶Æ¾¼ĆŌö³¤£¬Ä³ŹŠ¾ö¶ØŠĀ½ØŅ»ÅśÖŲµć¹¤³Ģ£¬·Ö±šĪŖ»ł“”É菩¹¤³Ģ”¢ĆńÉś¹¤³ĢŗĶ²śŅµ½ØÉč¹¤³ĢČżĄą£¬ÕāČżĄą¹¤³ĢĖłŗ¬ĻīÄæµÄøöŹż·Ö±šÕ¼×ÜŹżµÄ![]() ”¢
Ӣ![]() Ӣ
”¢![]() .ĻÖÓŠ3Ćū¹¤ČĖ¶ĄĮ¢µŲ“ÓÖŠČĪŃ”Ņ»øöĻīÄæ²ĪÓė½ØÉč.Ēó£ŗ
.ĻÖÓŠ3Ćū¹¤ČĖ¶ĄĮ¢µŲ“ÓÖŠČĪŃ”Ņ»øöĻīÄæ²ĪÓė½ØÉč.Ēó£ŗ
£ØI£©ĖūĆĒŃ”ŌńµÄĻīÄæĖłŹōĄą±š»„²»ĻąĶ¬µÄøÅĀŹ£» w.w.w.k.s.5.u.c.o.m ![]()
![]()
£ØII£©ÖĮÉŁÓŠ1ČĖŃ”ŌńµÄĻīÄæŹōÓŚĆńÉś¹¤³ĢµÄøÅĀŹ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
£Ø±¾Š”ĢāĀś·Ö12·Ö£©
ijĆńÓŖĘóŅµÉś²śA£¬BĮ½ÖÖ²śĘ·£¬øł¾ŻŹŠ³”µ÷²éŗĶŌ¤²ā£¬A²śĘ·µÄĄūČóÓėĶ¶×Ź³ÉÕż±Č£¬Ęä¹ŲĻµČēĶ¼1£¬B²śĘ·µÄĄūČóÓėĶ¶×ŹµÄĖćŹõĘ½·½øł³ÉÕż±Č£¬Ęä¹ŲĻµČēĶ¼2£¬
£Ø×¢£ŗĄūČóÓėĶ¶×Źµ„Ī»ŹĒĶņŌŖ£©
£Ø1£©·Ö±š½«A£¬BĮ½ÖÖ²śĘ·µÄĄūČó±ķŹ¾ĪŖĶ¶×ŹµÄŗÆŹż£¬²¢Š“³öĖüĆĒµÄŗÆŹż¹ŲĻµŹ½.£Ø2£©øĆĘóŅµŅŃ³ļ¼Æµ½10ĶņŌŖ׏½š£¬²¢Č«²æĶ¶Čėµ½A£¬BĮ½ÖÖ²śĘ·µÄÉś²ś£¬ĪŹ£ŗŌõŃł·ÖÅäÕā10ĶņŌŖĶ¶×Ź£¬²ÅÄÜŹ¹ĘóŅµ»ńµĆ×ī“óĄūČó£¬Ęä×ī“óĄūČóĪŖ¶ąÉŁĶņŌŖ.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com