
 为圆心,
为圆心,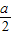 为半径的圆的极坐标方程是 .
为半径的圆的极坐标方程是 .  ),则OP=ρ,∠POA=θ-
),则OP=ρ,∠POA=θ- ,OA=2×
,OA=2×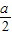 =a,Rt△OAP中,由OP=OAcos∠POA,化简可得圆的极坐标方程.
=a,Rt△OAP中,由OP=OAcos∠POA,化简可得圆的极坐标方程.
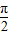 ),则OP=ρ,∠POA=θ-
),则OP=ρ,∠POA=θ- ,OA=2×
,OA=2× =a,
=a, )=asinθ,
)=asinθ, ,OA=2×
,OA=2× =a,是解题的关键,属于中档题.
=a,是解题的关键,属于中档题. 

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| a |
| 2 |
| π |
| 2 |
| a |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
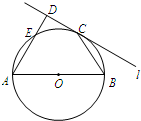 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
|
|
| π |
| 2 |
| π |
| 4 |
| a2+b2 |
| c2+d2 |
| (ac+bd)(ad+bc) |
查看答案和解析>>
科目:高中数学 来源: 题型:
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
|
|
| π |
| 4 |
| 2 |
| c |
| 4 |
| c |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
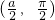 为圆心,
为圆心, 为半径的圆的极坐标方程是________.
为半径的圆的极坐标方程是________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com