
分析 (1)有放回的取球,根据分步计数原理可知有16种结果,满足条件的比较多不好列举,可以从他的对立事件来做.
(2)关键是要找出(m,n)对应图形的面积,及满足条件“关于x的一元二次方程x2-$\sqrt{2n}$x+m=0有实根”的点对应的图形的面积,然后再结合几何概型的计算公式进行求解.
解答  解:(1)先从袋中随机取一个球,记下编号为m,
解:(1)先从袋中随机取一个球,记下编号为m,
放回后,再从袋中随机取一个球,记下编号为n,
其一切可能的结果(m,n)有:
(1,1),(1,2),(1,3),(1,4),
(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),
(4,1),(4,2),(4,3),(4,4),共16个.
又满足条件n≥m+2的事件为:
(1,3),(1,4),(2,4),共3个,
所以满足条件n≥m+2的事件的概率为P1=$\frac{3}{16}$.
故满足条件n<m+2的事件的概率为1-P1=1-$\frac{3}{16}$=$\frac{13}{16}$;
(2)试验的全部结果所构成的区域为{(m,n)|0<m<1,0<n<1}(图中矩形所示).其面积为1.
构成事件“关于x的一元二次方程x2-$\sqrt{2n}$•x+m=0有实根”的区域为
{{(m,n)|0<m<1,0<n<1,n≥2m}(如图阴影所示).面积为$\frac{1}{2}×\frac{1}{2}×1$=$\frac{1}{4}$
所以所求的概率为$\frac{1}{4}$.
点评 本小题主要考查古典概念、对立事件的概率计算,考查几何概型,考查学生分析问题、解决问题的能力.能判断一个试验是否是古典概型,分清在一个古典概型中某随机事件包含的基本事件的个数和试验中基本事件的总数.


科目:高中数学 来源: 题型:解答题
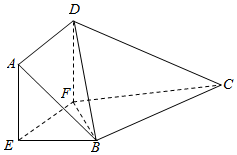 在直角梯形ABCD中,AB∥DC,AD⊥AB,DC=3,AB=2,AD=1,AE=EB,DF=1,现把它沿FE折起,得到如图所示几何体,连接DB,AB,DC,使DC=$\sqrt{5}$,
在直角梯形ABCD中,AB∥DC,AD⊥AB,DC=3,AB=2,AD=1,AE=EB,DF=1,现把它沿FE折起,得到如图所示几何体,连接DB,AB,DC,使DC=$\sqrt{5}$,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{2}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱的侧面积为16π
如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱的侧面积为16π查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{7\sqrt{2}}}{10}$ | B. | $\frac{{7\sqrt{2}}}{10}$ | C. | $-\frac{{\sqrt{2}}}{10}$ | D. | $\frac{{\sqrt{2}}}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com