
| |||||||||||||||
(1) |
解:曲线C在Bn(an,bn)的切线BnAn+1斜率为:
kn= 又∵kn= ∴ ∴{an}为等比数列,公比为 ∴{an}的通项an= |
(2) |
由(Ⅰ)知bn= ∴Sn= ∴ 解得:32< |
(3) |
解:由(Ⅱ)知,数列{Sn}是等比数列,首项S1= ∴Tn= ∴ ∴Tn=1- ∴8ncn=(8ncn-8n-1cn-1)+(8n-1cn-1-8n-2cn-2)+…+(83c3-82c2)+(82c2-8c1)+8c1 =(8n-1-1)+(8n-2-1)+…(82-1)+(8-1)+8c1 = ∴所求通项cn= [评析]:在等差数列中,若 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2004年高考教材全程总复习试卷·数学 题型:044
如图所示,已知圆的方程是(x-1)2+y2=1,四边形PABQ为该圆内接梯形,底边AB为圆的直径且在x轴上,以A,B为焦点的椭圆C过P,Q两点.
(1)若直线QP与椭圆C的右准线相交于点M,求点M的轨迹方程;
(2)当梯形PABQ周长最大时,求椭圆C的方程.

查看答案和解析>>
科目:高中数学 来源:2004年高考教材全程总复习试卷·数学 题型:044
如图所示,椭圆方程为 +
+ =1(a>b>0),A,P,F分别为左顶点,上顶点,右焦点,E为x轴正方向上一点,且|
=1(a>b>0),A,P,F分别为左顶点,上顶点,右焦点,E为x轴正方向上一点,且| |,|
|,| |,|
|,| |成等比数列.又点N满足
|成等比数列.又点N满足 =
= (
( +
+ ),PF的延长线与椭圆的交点为Q,过Q与x轴平行的直线与PN的延长线交于M.
),PF的延长线与椭圆的交点为Q,过Q与x轴平行的直线与PN的延长线交于M.
(1)求证: ·
· =
= ·
· .
.
(2)若 =2
=2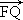 ,且|
,且| |=
|= ,求椭圆方程.
,求椭圆方程.

查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:047
如图所示,SA⊥正方形ABCD所在平面,过A作与SC垂直的平面分别交SB、SC、SD于E、K、H,求证:E、H分别是点A在直线SB和SD上的射影.

查看答案和解析>>
科目:高中数学 来源:湖南省十校联考2007届高三理科数学试题 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源:2007届潜山中学理复(一、二)数学周考试卷 题型:044
| |||||||||||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com