
【题目】已知椭圆W: ![]() (a>b>0)的上下顶点分别为A,B,且点B(0,﹣1).F1 , F2分别为椭圆W的左、右焦点,且∠F1BF2=120°.
(a>b>0)的上下顶点分别为A,B,且点B(0,﹣1).F1 , F2分别为椭圆W的左、右焦点,且∠F1BF2=120°.
(Ⅰ)求椭圆W的标准方程;
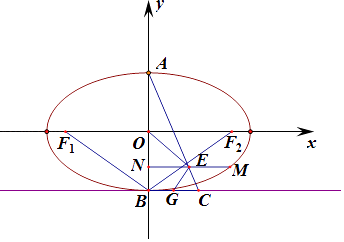
(Ⅱ)点M是椭圆上异于A,B的任意一点,过点M作MN⊥y轴于N,E为线段MN的中点.直线AE与直线y=﹣1交于点C,G为线段BC的中点,O为坐标原点.求∠OEG的大小.
【答案】解:(Ⅰ)依题意,得b=1.又∠F1BF2=120°,
在Rt△BF1O中,∠F1BO=60°,则a=2.
∴椭圆W的标准方程为 ![]() .
.
(Ⅱ)设M(x0,y0),x0≠0,则N(0,y0),E ![]() .
.
由点M在椭圆W上,则 ![]() .即
.即 ![]() .
.
又A(0,1),则直线AE的方程为 ![]() .
.
令y=﹣1,得C ![]() .
.
又B(0,﹣1),G为线段BC的中点,则G ![]() .
.
∴ ![]() ,
, ![]() .
.
∵ ![]() =
= ![]()
= ![]() =1﹣y0﹣1+y0=0,
=1﹣y0﹣1+y0=0,
∴ ![]() .则∠OEG=90°,
.则∠OEG=90°,
∠OEG为90°.
【解析】(Ⅰ)由b=1,由∠F1BO=60°,则a=2.即可求得椭圆W的标准方程;(Ⅱ)由题意设N和E点坐标,设直线AE的方程,当y=﹣1,即可求得C点坐标,求得G点坐标,则 ![]() ,
, ![]() .根据向量数量积的坐标运算,即可求得
.根据向量数量积的坐标运算,即可求得 ![]()
![]() =0,则
=0,则 ![]() ,则∠OEG=90°.
,则∠OEG=90°.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示,若将运动员按成绩由好到差编为![]() 号,再用系统抽样方法从中抽取7人,则其中成绩在区间
号,再用系统抽样方法从中抽取7人,则其中成绩在区间![]() 上的运动员人数是
上的运动员人数是 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+a|+|x﹣2|
(1)当a=﹣3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x﹣4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列几个命题:
①函数![]() 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
②方程![]() 的有一个正实根,一个负实根,
的有一个正实根,一个负实根,![]() ;
;
③![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() ,则
,则![]() 时,
时,![]()
④函数![]() 的值域是
的值域是![]() .
.
其中正确命题的序号是_____(把所有正确命题的序号都写上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sinωx(ω>0)的图象向左平移 ![]() 个单位得到函数g(x)的图象,若函数g(x)的图象关于直线x=ω对称且在区间(﹣ω,ω)内单调递增,则ω的值为( )
个单位得到函数g(x)的图象,若函数g(x)的图象关于直线x=ω对称且在区间(﹣ω,ω)内单调递增,则ω的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD=2DC,四边形ABEF是正方形,且平面ABEF⊥平面ABCD,M为AF的中点, (I)求证:AC⊥BM;
(II)求异面直线CE与BM所成角的余弦值.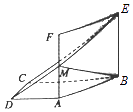
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且(c+b)(sinC﹣sinB)=a(sinA﹣sinB).若c=2 ![]() ,则a2+b2的取值范围是 .
,则a2+b2的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 过F2作一条直线(不与x轴垂直)与椭圆交于A,B两点,如果△ABF1恰好为等腰直角三角形,该直线的斜率为( )
=1(a>b>0)的左、右焦点分别为F1 , F2 , 过F2作一条直线(不与x轴垂直)与椭圆交于A,B两点,如果△ABF1恰好为等腰直角三角形,该直线的斜率为( )
A.±1
B.±2
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com